Распределения Пирсона и Стьюдента

Познакомимся с двумя наиважнейшими распределениями математической статистики.

1. Распределение 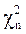(²хи-квадрат²) Пирсона. Так называется распределение случайной величины, равной

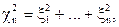(2.29)

где xi- независимые, нормально распределённые, стандартные N(0,1) случайные величины. Число слагаемых n называется числом степеней свободы этого распределения.

Это распределение хорошо изучено и для него существуют подробные таблицы.

Распределение Стьюдента (t-распределение).Пусть x, x₁, ... , x_n- независимые нормальные стандартные случайные величины. Распределением Стьюдента с n степенями свободы называется распределение случайной величины

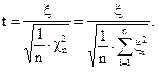(2.30)

Распределение Стьюдента также хорошо изучено и для него тоже существуют подробные таблицы. Это распределение симметрично относительно 0 и при больших n мало отличается от нормального. Методика работы с ним в точности соответствует той, которую мы применяли при работе с нормальным распределением. Аналогом значений k_bнормального распределения являются значения t_n,b(при пользовании таблицами надо учитывать число степеней свободы n), которые в задачах статистики принято называть критическими значениями. В таблице6 (см. приложение) заданы t_n,b, которые являются корнем решения уравнения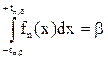, где f_n(x) – плотность вероятности распределения Стьюдента с n степенями свободы для b=0,9; 0,95; 0,98; 0,99, а также корни решения уравнения 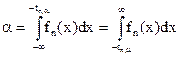для a=0,05; 0,025; 0,01; 0,005.

Можно сравнить нижнюю строку таблицы 6, соответствующую бесконечному числу степеней свободы, со значениями k_bнормального распределения, чтобы убедиться в “похожести” распределения Стьюдента и нормального.

Распределение Стьюдента широко применяется в статистике. Приведем примеры решения задач, к которым сводится большое количество статистических задач, решаемых в экономике.

Пример. Найти такой интервал (-a,a), вероятность попадания в который случайной величины, распределенной по Стьюденту с 10-ю степенями свободы (обозначаемой t₁₀), равна 0,90. То есть найти а из уравнения Р{-a<t₁₀<a}=0,90.

Решение. В таблице 6, задающей значение 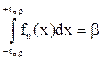, находим значение, соответствующее n=10 и b=0,9. Это 1,81, следовательно, искомый интервал (–1,81, 1,81).

Пример. Найти такой полуинтервал (-¥,-a), для которого вероятность того, что величина, распределенная по Стьюденту с 18-ю степенями свободы (t₁₈), попадает в него (т.е. ее значение не превосходит значения –a), равна 0,025. Т.е. надо решить уравнение .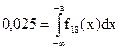

Решение. В таблице 6 отыскиваем в нижней строке число 0,025, это даст нам нужный столбец, в строке с n=18 в этом столбце находим значение 2,1. Нужное нам значение a находится в нижней строке, а не в верхней, в силу того, что решается уравнение .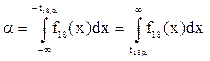

Ответ: P{t₁₈<-2,1}=0,025.

Дата добавления: 2014-03-11; просмотров: 584; Нарушение авторских прав

Мы поможем в написании ваших работ!