ТЕПЛОВАЯ ТЕОРЕМА НЕРНСТА

Сопоставление тепловых эффектов и изменения энергии Гиббса в реакциях, происходящих в конденсированных системах при различных температурах, показывает, что в области низких температур при приближении к абсолютному нулю значения тепловых эффектов и изменения энергии Гиббса сближаются. Тепловая теорема является постулатом, утверждающим, что это сближение продолжается и при дальнейшем понижении температуры, причем при абсолютном нуле и вблизи него кривые соприкасаются и общая для них касательная параллельна оси температур.

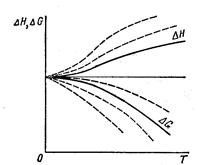
Математически ΔG = ΔH

lim│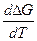│_T→0 = lim│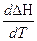│_T→0 = 0

Из тепловой теоремы вытекает ряд следствий

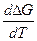()_p = -ΔS при Т → 0

lim[ΔS]_T→0 = 0 [ΔS]_T=0 = 0

т.е. вблизи абсолютного нуля все реакции, совершающиеся в конденсированных системах ,не сопровождаются изменением энтропии.

Второе следствие получим, применяя условие

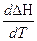()_p = ΔC

lim[ΔC]_T→0 = 0 [ΔC]_T=0 = 0

т.е. вблизи абсолютного нуля изменение теплоемкости твердых реагирующих веществ бесконечно мало отличается от нуля. Можно показать, что при очень низких температурах не только ΔS и ΔС твердых тел стремятся к нулю, но и многие другие свойства тел (объем, давление насыщенного пара и др.) изменяются с температурой так, что их производные по температуре стремятся к нулю. Этим объясняется принцип недостижимости абсолютного нуля (называемый также третьим законом термодинамики),согласно которому никакие процессы не могут снизить температуру до абсолютного нуля.

1.24 РАСЧЕТ ХИМИЧЕСКОГО РАВНОВЕСИЯ С ПОМОЩЬЮ

СТАНДАРТНЫХТЕРМОДИНАМИЧЕСКИХ ВЕЛИЧИН

В настоящее время известны стандартные теплоты образования и энтропии более 7500 простых веществ и соединений. С помощью этих табличных данных можно вычислить термодинамические параметры многих десятков тысяч реакций, в том числе предполагаемых и не изученных экспериментально. В методе расчета, основанном на использовании стандартных термодинамических величин, используются два исходных уравнения

ΔG⁰_T = ΔH⁰_T – TΔS⁰_T

lnK⁰_P = - ΔG⁰_T /RT

Если нет никаких предварительных сведений о положении равновесия при интересующей нас температуре, расчет ΔG и Кр полезно производить в две стадии. В первой стадии вычисляют изменение энергии Гиббса при Т = 298К и для стандартных условий.

Для расчета ΔН⁰₂₉₈ и ΔS⁰₂₉₈ используют уравнения

ΔH⁰₂₉₈ = (nΔH⁰_298,f)_кон - (nΔH⁰_298f)_нач

ΔS⁰₂₉₈ = (nS⁰₂₉₈)_кон - (nS⁰₂₉₈)_нач

По величине и знаку ΔG⁰₂₉₈ судят о возможности получения желаемых веществ из взятых исходных в стандартных условиях.

Не следует думать, что реакция неосуществима вообще, если по расчету получится сравнительно небольшая величина ΔG⁰₂₉₈.Реакция невозможна только в стандартных условиях, но, вероятно, может протекать при иных температурах и давлении, при непрерывном удалении продуктов реакции из зоны реакции.

Точный расчет (вторая стадия) покажет - при каком сочетании указанных факторов величина энергии Гиббса станет отрицательной и как она должна быть изменена дальше, чтобы выход продуктов реакции сделался достаточно большим. В качестве ориентировочного критерия, определяющего целесообразность второго этапа расчетов, рекомендуется величина ΔG⁰₂₉₈ = 418кдж/моль

На второй стадии расчета переходят от значения ΔG⁰₂₉₈ к значению ΔG⁰_т при других температурах.

Для этого необходимо вычислить ΔH⁰_т и ΔS⁰_т при заданной Т.

ΔH⁰_т = ΔН⁰₂₉₈ + 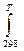ΔС_рdT

ΔS⁰_т = ΔS⁰₂₉₈ + 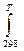ΔС_р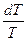

ΔG⁰_т = ΔH⁰₂₉₈ – TΔS⁰₂₉₈ + 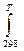ΔC_pdT - T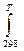ΔC_p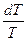

Если пренебречь влиянием изменения теплоемкости, т. е. ΔС_р = 0,то решение уравнения будет грубо приближенным

ΔG⁰_т = ΔH⁰₂₉₈ – TΔS⁰₂₉₈

Данное приближение (первое приближение Улиха) необходимо для быстрой оценки возможности протекания реакции при интересующей температуре.

При выполнении точного расчета подставляется зависимость

ΔС_р = f(T) ΔC_р = Δа + ΔвТ + ΔсТ² + Δс¹ Т^-2

Проведя интегрирование, получим

ΔG⁰ _т = ΔH⁰₂₉₈ – TΔS ⁰₂₉₈ - T{Δa(ln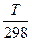+ 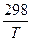- 1) +

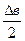+ (T - 2×298 + 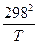) + 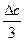(Т² - 3×298² + 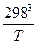) - Dс¹(-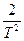

+ + )}.

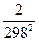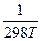DG⁰_T = DH⁰₂₉₈ - T×DS⁰₂₉₈ – T(DaM₀ + DbM₁ + DcM₂ + Dc¹M_-2.

Коэффициенты М₀ ,М₁ ,М₂ , М_-2 рассчитаны для разных температур, их значения можно найти в справочнике.

Этот метод расчета называется методом Темкина – Шварцмана.

Дата добавления: 2014-03-11; просмотров: 538; Нарушение авторских прав

Мы поможем в написании ваших работ!