
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Преобразований Лапласа
Решение линейных дифференциальных уравнений с помощью
Идея метода в том, что решение диф. уравнения из области функции действительного переменного f(t), переносится в область комплексного переменного.
Р = a +j*ω (область комплекс переменного)
где α- вещественная часть комплексного переменного;
j *ω— мнимая часть комплексного числа.
J означает корень из минус 1, где операции решения принимает более простой вид. Вместе диф. уравнение решается алгебраически.
Полученное операторное решение переводится обратно в область действительного переменного.
Формально символ дифференцирования d/ dt заменяется оператором р.
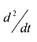 соответственно ---- +р2и т.д.
соответственно ---- +р2и т.д.
Символ интегрирования ƒdt заменяется 1/Р.
Функция времени f(t) соответственно преобразуется, называется оригиналом, а функция f(p), полученная в результате преобразования -изображение.
Символ р - называют оператором, форму записи уравнения -операторной.
Функция f(p) получается умножением f(t) на экспоненциальную
функцию е
F(p) = ƒf(t)*e-pt*αt
Пример: 1) Найти изображение функции времени f(t) = е –pt Напишем выражение преобразования функции Лапласа и проинтегрируем:
F(p) = ƒf(t) *e-pt *t = -l/(α+p) *e-(α+p)t = 1/(α+p)
2) оригинал функции имеет вид
Onput < О
Δлвых=----------
Anput > О
Изменение входной величины элемента или системы имеет
скачкообразный характер.
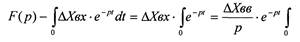
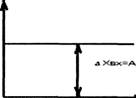
Для нахождения по оригинальной функции соответствующих изображений и по изображениям оригиналов существуют специальные таблицы преобразования Лапласа.
| F(t) оригинал | F(p) изображение |
| {1} | 1/Р |
| А{1} | А/Р |
| t | 1/p2 |
| t2 | 2/р4 |
| tn/n | 1/ Pm+1 |
| е±2t | /Р±а |
| sinαt | 1/ /(P2 +a2) |
| соsαt | P/(P2+a2) |
| t∙e-αt | 1/(py+α)y2y |
| t* sinat | α/(P + a)2+a2 |
| t*cosat | P+α/(P + a)2+a2 |
Динамическими звеньями являются: переходная функция, передаточные функции и частично передаточная функция или частные характеристики.
Переходной функцией Хвых(х) называют изменения выходной величины во времени, вызванное единичным скачкообразным изменением входной величины Хвх = 1.
Переходную функцию получают постановкой диф. уравнения или уравнения в операторной форме переходного процесса Хвх =1.
Для диф уравнения
T*dХХвы/dt+ТХХвы=КХвх
Предположим что Хвх = 1, то получим
dXXвы
Т + ТХХвы = К
dt
Но режим этого уравнения относительно Хвых, найдем по Лапласу его
изображение:
Тррхвы + ТХХвы = К
Хвых = К/Т((+1)переходная функция для диф. уравнения
Графически изображение переходных функций зависит от динамических свойств звена и характера внесенных воздействий, и имеет вид аналогичных переходным процессам только с уменьшением ординате в Хвх раз.
Передаточной функций w(p) звена или системы называют отношение изображения по Лапласу выходной величины к отношению изображения
входной величины при нулевых начальных условиях.
Передаточная функция из диф уравнения звена или системы записанной в операторной форме.
Так для диф уравнения
Т* dХХвы/dt+XХвх
Найдем изображение функции по Лапласу
Хвых(Тр +1) = КХвх
Разделим обе части на Хвх и решим относительно Vbx/Xbx:
Хвых/Хвх = К/Тp-1 =W(p)
Передаточная функция
Частотой характеристикой называют функцию частоты, описывающей изменение амплитуды и фазы гармонических колебаний выходной величины элемента. Частотные характеристики отличаются от функции входного воздействия только по амплитуде и фазе.
| <== предыдущая страница | | | следующая страница ==> |
| Динамические характеристики элементов | | | Типовые звенья САР и их характеристики |
Дата добавления: 2014-03-11; просмотров: 410; Нарушение авторских прав

Мы поможем в написании ваших работ!