
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Уравнение Пьера Лапласа
Двумя парами меридиональных и конических плоскостей выделим элемент оболочки.
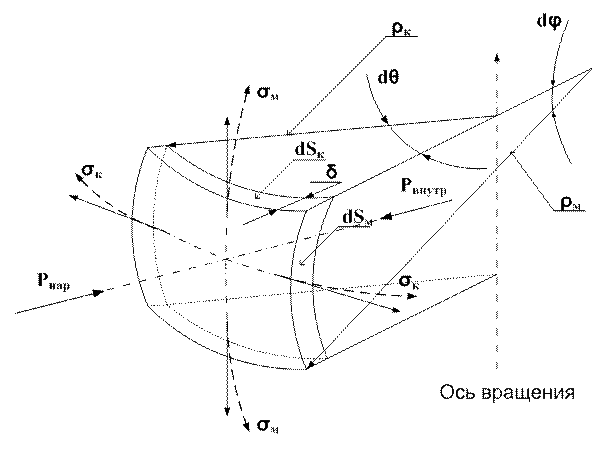
Обозначения:
σм - напряжения вдоль направления меридиана (меридиональные напряжения),
σк - напряжения по кольцевому сечению (окружные или кольцевые напряжения),
ρм - радиус дуги по меридиану,
ρк - радиус дуги кольцевого сечения,
δ - толщина оболочки,
Pвн- внутреннее давление,
Pн - наружное давление,
Избыточное внутренне давление (разность между внутренним и наружным давлениями)
P = Pвнутр - Pнар.
Элемент форму менять не может: отсутствуют касательные напряжения (т.к. касательные напряжения изменяют форму).
Под действием нормальных напряжений элемент может изменять размеры:
σм и σк – главные напряжения.
Составим уравнение выделенного элемента оболочки.
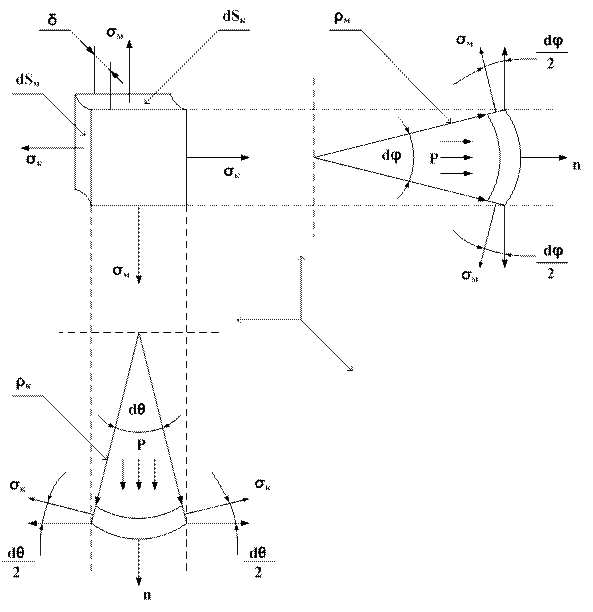
Условие равновесия: сумма сил на нормаль оболочки равна нулю.
∑ Nn = 0
P·dSм·dSк − σм·dSк·δ·sin 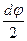 ·2 − σк·dSм·δ·sin
·2 − σк·dSм·δ·sin 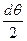 ·2 = 0, [н].
·2 = 0, [н].
т.к. углы малы, то:
sin 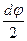 ≈
≈ 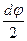
sin 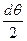 ≈
≈ 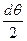 ;
;
длина дуги:
dSк = ρк·dθ
dSм = ρм·dφ.
P·dSм·dSк − σм·dSк·δ· 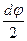 ·2 − σк·dSм·δ·
·2 − σк·dSм·δ· 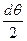 ·2 = 0
·2 = 0
P·dSм·dSк − σм·dSк·δ·dφ − σк·dSм·δ·dθ = 0
После замены синуса и сокращения ''2'' разделим на dSм·dSк·δ
P·dSм·dSк − σм·dSк·δ·dφ − σк·dSм·δ·dθ = 0 | : dSм·dSк·δ
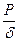 – σм·
– σм· 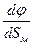 – σк·
– σк· 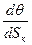 = 0
= 0
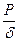 –
– 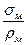 –
– 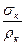 = 0
= 0 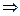
Уравнение равновесия элемента оболочки:
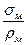
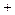
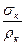
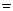
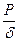 .
.
Тонкостенная оболочка противодействует внутреннему давлению за счёт кривизны поверхности (к плоским стенкам не применимо).
В этом уравнении два неизвестных, поэтому запишем уравнение отсечённой части оболочки:
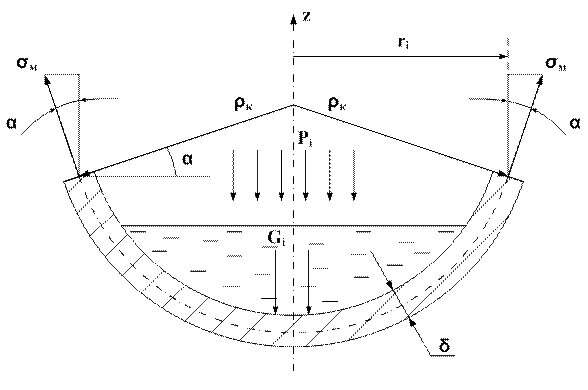
∑ Fz = 0
σм·cosα·2·π· ri·δ – Gi – Pi·π· ri2 = 0
Условие прочности.
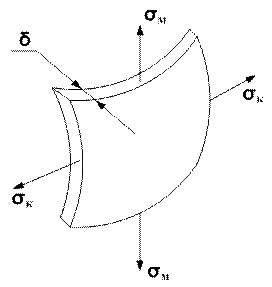
Стенка оболочки находится в двумерном напряжённом состоянии: это сложное напряжённое состояние.
Но для использования III-й гипотезы прочности это состояние необходимо свести к одномерному.
σэквIII = σ1 – σ3 ≤ [σ],
где: σ1 > σ2 > σ3 (в алгебраическом смысле);
σм и σк – главные нормальные напряжения,
σкас – касательное напряжение.
Но, пренебрегая взаимным давлением молекул друг на друга в стенке, толщиной δ, примем σкас ≈ 0.
Пример: Цилиндрический сосуд находится под воздействием внутреннего давления.
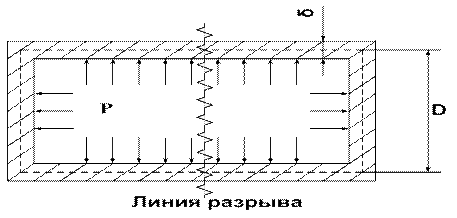
Дано: D, δ, P.
Определить: σм, σк.
1.
∑ Fz = 0
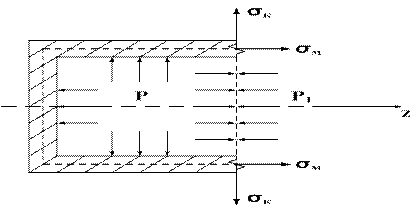
σм·π·D·δ – P1· 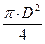 = 0
= 0
Следует помнить, что
Sкольца = π·D·δ, а Sкруга = 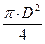 .
. 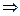
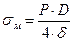 .
.
2.Уравнение Лапласа для цилиндра: 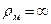
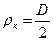
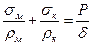
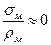
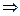
 →
→
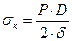 .
.
Выводы:
▪ В цилиндре кольцевые напряжения в два раза больше чем меридиональные (поэтому зимой трубы лопаются вдоль, а не пополам).
▪ Цилиндрический сосуд с меньшим диаметром при одинаковой толщине стенок выдерживает большее давление.
Устойчивость оболочек.
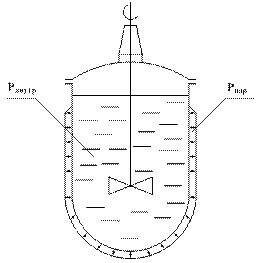
Цилиндрические сосуды подразделяются на две группы: длинные и короткие.
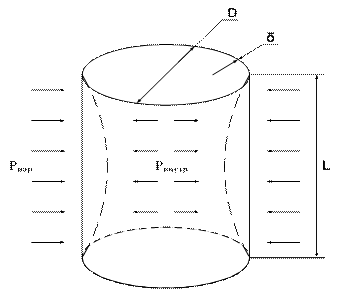
Граничная длина: 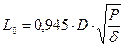
L > L0 – ''длинные'',
L < L0 – ''короткие''.
У длинных и коротких сосудов по-разному происходит потеря устойчивости.
''Длинный'' цилиндрический сосуд.
Две волны: P(2)критическое.


''Короткий'' цилиндрический сосуд.
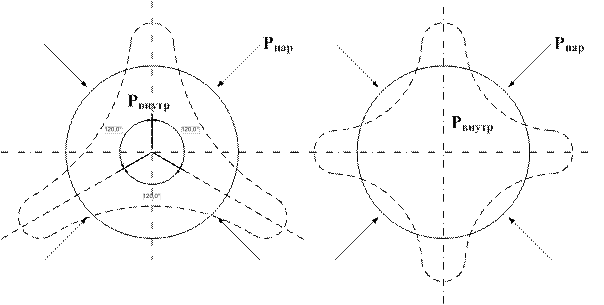
Три волны: 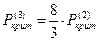 . Четыре волны:
. Четыре волны: 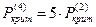 .
.
Короткий цилиндрический сосуд выдерживает большее давление, чем длинный при одинаковой толщине стенок, давлении и диаметре.
Критическое наружное давление можно рассчитать по формуле Попковича:
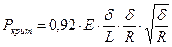 .
.
Запас прочности приближённо определяется из соотношения:
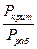 ≈ 1,5 ÷ 2,5.
≈ 1,5 ÷ 2,5.
Замечание о конструктивном решении.
Как правило, запас по критическому давлению достигается не за счёт толщины стенки изделия, а за счёт продольных и поперечных рёбер жёсткости.

Напряжения в оболочках.
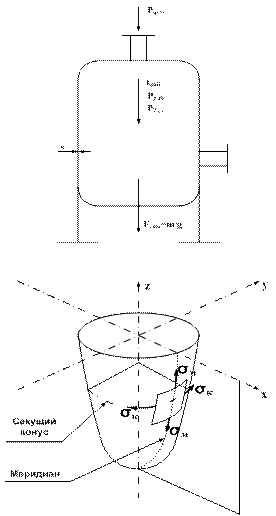
По законам механики: силы внутреннего давления, действующие на элементарную поверхность, уравновешиваются усилиями, приложенными по краям, касательными, поперечными силами и изгибающими моментами.
Учесть в процессе расчёта все нюансы механики (теория моментов) сложно, поэтому, пренебрегая действием изгибающих моментов и поперечных сил, расчёт ведут по мембранной теории (при этом Sаппарата -толщина стенки- очень мала по сравнению с длиной, а напряжение равномерно распределено по толщине).
Силы, действующие по касательной к окружности, называют кольцевыми, а по касательной к меридиану – меридиональными (осевыми), при этом кольцевые силы вызывают кольцевые напряжения, а меридиональные – меридиональные напряжения.
1). Для закрытого цилиндра:
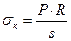 ,
, 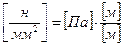
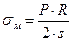
при вертикальном положении сосудов:
P = h·γ 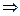
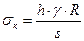 , где:
, где:
γ – удельный вес жидкости, 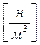 ;
;
R – средний радиус цилиндра, [м];
s – толщина стенки, [м].
2). Для сферического аппарата:
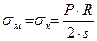
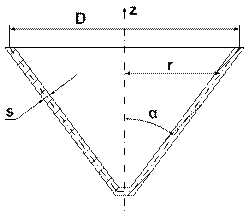
3). Для конического аппарата:
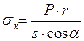
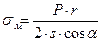 , где:
, где:
r – средний радиус кольца в точке определения напряжения [м];
α – угол между осью вращения и образующей конуса.
Напряжения σк и σм достигают максимального значения при 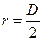 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Тонкостенные сосуды | | | Краевые распорные силы |
Дата добавления: 2014-08-04; просмотров: 662; Нарушение авторских прав

Мы поможем в написании ваших работ!