
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Оценка качества регрессионной модели в целом
Под качеством регрессионной модели понимается значимость модели в целом и её параметров, а также ошибка моделирования.
Для оценки качества модели в целом используется коэффициент детерминации, который в общем случае определяется как
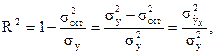
где 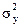 - общая дисперсия результатного признака,
- общая дисперсия результатного признака,
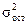 - остаточная дисперсия,
- остаточная дисперсия,
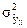 - дисперсия объясняющей части общей дисперсии.
- дисперсия объясняющей части общей дисперсии.
Чем ближе 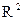 к 1, тем выше качество регрессионной модели.
к 1, тем выше качество регрессионной модели.
В случае линейной регрессии:
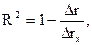
где 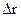 - определитель матрицы парных коэффициентов корреляции,
- определитель матрицы парных коэффициентов корреляции,
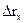 - определитель матрицы межфакторной корреляции.
- определитель матрицы межфакторной корреляции.
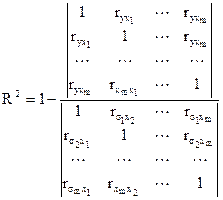
Для двухфакторной модели
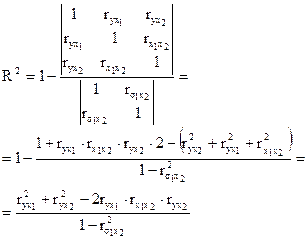
Другим способом оценки качества регрессионной модели в целом является использование F-критерия Фишера, определяемого как 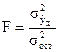
Тем самым величина F-критерия связана с коэффициентом детерминации, а именно 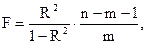
где m – число параметров при переменной х, в линейной модели совпадает с числом включенных в модель факторов;
n – число наблюдений.
Для двухфакторной (парной) модели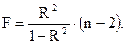
Значение полученного фактического F-критерия сравнивается с табличным значением на уровне α = 0,05, и если 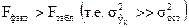 , то модель в целом считается значимой (существенной).
, то модель в целом считается значимой (существенной).
2.9. Оценка значимости факторов, включаемых в модель множественной регрессии
Кроме значимости уравнения регрессии в целом, оценивается так же значимость каждого фактора, включенного в регрессионную модель. Незначимые факторы включать в модель нецелесообразно.
Для оценки значимости коэффициентов регрессии используется t-критерий Стьюдента:
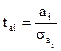 ,
,
где – СКО коэффициента регрессии 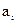 , которое может быть определено как
, которое может быть определено как
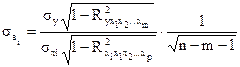
При использовании пакета программ статистического анализа программа наряду с регрессионной моделью выведет сообщения о значимости как всей зависимости в целом, так и о значимости каждого параметра модели. Пусть необходимо построить модель по следующим данным:
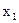
| 6,3 | 5,9 | 8,6 | 5,1 | 6,4 | 9,3 |
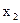
| 7,2 | 4,3 | 1,5 | 3,6 | 5,4 | 2,6 |
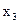
| 25,6 | 15,8 | 23,3 | 31,6 | 15,9 | 18,6 |
| y | 6,3 | 3,5 | 1,2 | 2,6 | 4,9 | 1,5 |
Будет получено следующее решение:
Зависимость 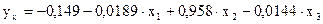
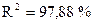
| Параметры | Значения параметров | СКО
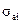
| t – статистика | 
|
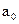
| -0,149 | -0,074 | 0,95 | |
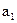
| -0,0189 | 0,168 | -0,112 | 0,92 |
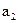
| 0,958 | 0,129 | 7,42 | 0,02 |
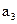
| -0,0144 | 0,0359 | -0,402 | 0,727 |
| Наименование | Сумма квадратов (девиация) | D.f. (степени свободы) | Дисперсия | F-критерий | α |
| Модель(yx) | 19,32 | 6,44 | 30,86 | 0,0315 | |
| Остатки(Σ) | 0,42 | 0,21 | |||
| Всего | 19,73 |
Ниже можно сделать выводы.
В целом модель существенна, т.к. 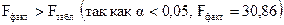 , т.е. объясняющая дисперсия гораздо больше остаточной.
, т.е. объясняющая дисперсия гораздо больше остаточной.
Действительно, так как  , то:
, то:
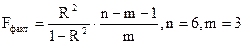
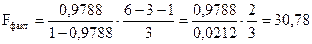 (ошибки округления).
(ошибки округления).
t - статистика в данном случае показывает, во сколько раз значение параметра больше, чем СКО параметра.
Если значение параметра меньше, чем СКО параметр, то параметр незначим, даже если параметр больше СКО, но 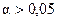 , то это превышение недостаточно. Только параметр
, то это превышение недостаточно. Только параметр 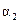
является значительным, так как 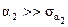 (в 7,42 раза) и
(в 7,42 раза) и 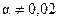 . Таким образом, значимость модели в целом достигается лишь за счет параметра
. Таким образом, значимость модели в целом достигается лишь за счет параметра 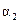 .
.
Проанализируем переменные.
Матрица парных коэффициентов:
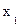
| 
| 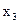
| 
| |
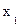
| 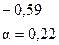
| 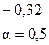
| 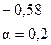
| |

| 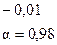
| 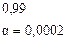
| ||
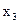
| 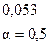
| |||

|
Видно, что очень сильная связь между y и 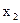 , остальные коэффициенты корреляции незначимы.
, остальные коэффициенты корреляции незначимы.
Вообще говоря, целесообразно рассмотреть парную модель 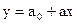 , где
, где 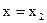 .
.
Получим 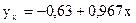
 , F=170,81,
, F=170,81, 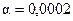 , т.е. модель в целом значима.
, т.е. модель в целом значима.
| Параметры | Значения параметров | СКО
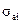
| t – статистика | 
|
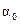
| -0,63 | 0,33 | -1,9 | 0,13 |
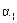
| 0,967 | 0,074 | 13,1 | 0,0002 |
Так как для 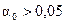 , то этот параметр незначим (в данном случае, т.е. в случае парной регрессии, значимость параметра a, и значимость модели в целом совпадает),
, то этот параметр незначим (в данном случае, т.е. в случае парной регрессии, значимость параметра a, и значимость модели в целом совпадает), 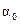 незначим в силу малого числа наблюдений.
незначим в силу малого числа наблюдений.
Этот пример наглядно показывает, что учет множества факторов не всегда приводит к адекватной модели, наоборот, сокращение числа факторов может улучшить модель.
В рассмотренном примере легко перейти от приведенных коэффициентов к структурным:
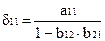
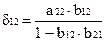

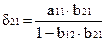
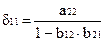
Откуда:
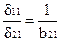 или
или 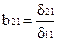
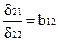
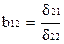
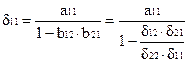
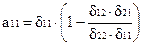
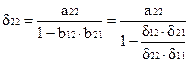
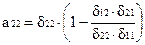
Например, уравнение в структурной форме:
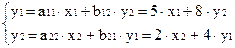
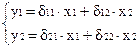
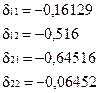
Приведенная форма:
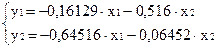
обратный переход дает прежние значения коэффициентов a11, a22, b12 , b21.
| <== предыдущая страница | | | следующая страница ==> |
| Виды моделей нелинейной регрессии | | | Оценка погрешности регрессионной модели |
Дата добавления: 2014-03-19; просмотров: 1395; Нарушение авторских прав

Мы поможем в написании ваших работ!