Линейные траектории

Типы временных траекторий

Системно-динамическое моделирование отображает динамическое поведение систем, т. е. их поведение во времени. В системной динамике разработчик модели старается идентифицировать образцы поведения, демонстрируемые ключевыми переменными, и затем строит модель, которая может воспроизвести заданные образцы. Если модель обладает этой способностью, она может использоваться как лабораторный инструмент для тестирования политик, нацеленных на изменение системного поведения желательным образом.

Хотя реальные системы могут демонстрировать разнообразные временные траектории (часто одновременно), число выделяемых «семейств» временных траекторий сравнительно невелико. Существует четыре «чистых» типа траекторий:

1) линейные (рис. 9);

2) экспоненциальные (рис. 10);

3) телеологические (целестремительные) (рис. 11);

4) колебательные (рис. 12).

Их комбинации порождают большое количество смешанных типов. Для нас важна связь выделенных типов динамического поведения с соответствующими фрагментами структурных диаграмм системно-динамических моделей.

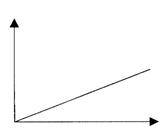
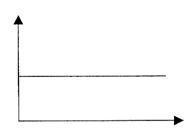
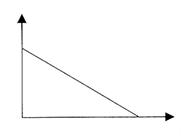
Первое идентифицируемое семейство временных траекторий – линейное. Линейное семейство включает линейный рост (рис. 9 а), равновесие (рис. 9 б) и линейный упадок (рис. 9 в).

а	б	в

Рисунок 9 – Семейство линейных траекторий

Большинство систем растут и приходят в упадок не линейно, а, скорее, по экспоненциальным траекториям, как показано на рисунке 10. Чистые линейные траектории обычно генерируются системами, в которых нет обратной связи между переменной состояния системы и её чистым приростом: он остается постоянным, даже если значение переменной состояния меняется. То, что принимают за линейный рост, часто оказывается экспоненциальным ростом, но рассматриваемым на слишком коротком отрезке времени, чтобы можно было заметить ускорение.

Равновесная траектория, (рис. 9 б) − это тип динамического поведения, который редко демонстрируют реальные системы. Это состояние идеального равновесия, в котором нет импульсов к изменению. Фактически, с системно-динамической точки зрения равновесие предполагает, что все переменные состояния системы достигают своих желательных значений одновременно – это искусственная ситуация.

Необходимо различать статическое и динамическое равновесие. В системно-динамической модели уровень (переменная состояния) находится в равновесии, если разность входного и выходного потоков равна нулю. Это ситуация динамического равновесия, поскольку содержимое накопителя все время меняется. Статическое равновесие имеет место, когда входной и выходной потоки равны нулю: в накопитель ничего не поступает и из него ничего не выходит.

Дата добавления: 2014-03-21; просмотров: 436; Нарушение авторских прав

Мы поможем в написании ваших работ!