Элементы теории поля. Определение векторного поля

Векторная функция, отображающая .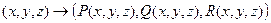

Градиент скалярной функции - векторная функция: , ,

Пример: 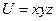- тогда .

называется потенциалом поля

Потенциальное поле: Если существует такая U(x,y,z), что , , (то есть их общая первообразная), векторное поле называется потенциальным, U(x,y,z) - его потенциал.

Свойство. Если U - потенциал, то U+C - тоже потенциал.

Доказательство: , ,

Теорема 1. Поле F потенциально симметрична производная матрица .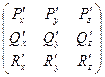

ДОКАЗАТЕЛЬСТВО.

, , , тогда

=

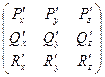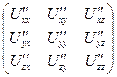
потому что , ,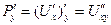

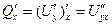Но (!!!) эти смешанные частные производные 2-го порядка совпадают, значит, = .

Аналогично 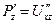= 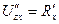. Аналогично = .

Итак, 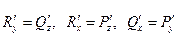и матрица симметрична.

Определение. Дивергенция векторного поля.

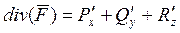(сумма элементов главной диагонали производной матрицы).

Определение Ротор векторного поля.

rot(F) = = .

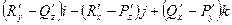Куда направлен ротор (чертёж на доске для векторного поля (-y,x,0) ).

Определение. Если ротор = 0 то поле называется безвихревым.

Следствие. Векторное поле F потенциально его ротор = 0.

ДОКАЗАТЕЛЬСТВО.

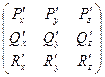симметрична

= .

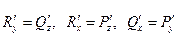
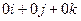Следствие (для плоского поля). Векторное поле в R² потенциально .

Определение. Работа векторного поля при перемещении точки по замкнутому контуру называется циркуляцией.

Обозначение: или

ЛЕММА. Криволинейный интеграл 2 рода от F не зависит от пути циркуляция = 0.

ДОКАЗАТЕЛЬСТВО.

Необходимость.

Если то то .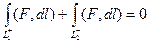

Но так как объединение 2 частей в замкнутый контур 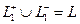, тогда и получается

.

Достаточность.

Если 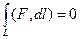, разобъём контур на 2 части какими-нибудь 2 точками А,В.

Возникают 2 части, и 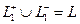, тогда , значит значит . Что и требовалось доказать.

Теорема 2. Поле F потенциально Криволинейный интеграл 2 рода от F не зависит от пути.

Примечание. Потенциал в точке А вычисляется как U(А)-U(A₀), где A₀ - начальная точка, как правило (0,0,0).

ДОКАЗАТЕЛЬСТВО.

Необходимость. Если поле потенциально то , ,

а тогда в интеграле 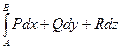получится 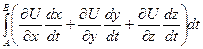а по формуле полного дифференциала это 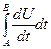но ведь первообразная от производной - это сама функция U, тогда работа поля 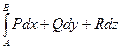в итоге равна 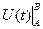= 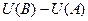то есть зависит только от начальной и конечной точки.

Достаточность.

Если криволинейный интеграл для поля (P,Q,R) не зависит от пути, возьмём начальную точку, например начало координат (0,0,0). Введём скалярную функцию U(x,y,z) равную работе поля от (0,0,0) до точки А(x,y,z). То есть .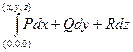

Составим путь из дуги от 0 до А и дополнительного маленького горизонтального отрезка вдоль оси Ох. Интеграл от 0 до А равен U(А). Интеграл от 0 до А₁ равен U(А₁).

Их координаты А (x,y,z) А₁ (x+∆x,y,z) .

=

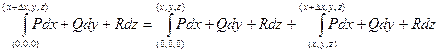но в интеграле по отрезку АА₁ меняется только x,

при этом y, z константы, то есть dy = 0, dz = 0.

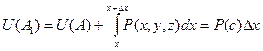для некоторой промежуточной точки с, где достигается среднее значение. Тогда , = . Но точка с тоже стремится к х при ∆x →0.

То есть . Итак, .

Аналогично , .

Алгоритм нахождения потенциала, пример.

Пример. 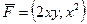. Доказать, что поле потенциально, и найти потенциал.

= .

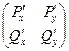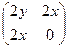Итак, эта матрица симметрична, значит, поле потенциально.

Теперь ищем потенциал. Для этого вычислим криволинецный интеграл от точки (0,0) до произвольной точки (x,y). Так как он не зависит от пути, выберем для простоты ломаную, так чтобы отрезки были вдоль осей

= = = .

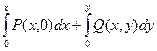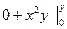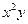В пространстве было бы .

Интегральные формулы.

Формула Грина. .

Пример вычисления работы по единичной окружности от поля F = (-y,x) без формулы и по формуле Грина.

Формула Стокса .

Формула Остроградского-Гаусса. .

Дата добавления: 2014-07-30; просмотров: 411; Нарушение авторских прав

Мы поможем в написании ваших работ!