
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Реологические модели Земли
Реология – это наука о поведении неидеально упругих тел под действием приложенных к ним нагрузок (напряжений).
В идеально упругом теле затухания упругих колебаний происходить не должно. Однако анализ распространения сейсмических волн в теле Земли показывает, что амплитуды этих волн заметно уменьшаются по мере удаления от источника. Таким образом, Земля – это неидеально упругое тело даже по отношению к колебаниям частоты герцового диапазона (периоды сейсмических волн порядка 0,01–1 с).
По отношению же к нагрузкам, которые действуют на Землю в геологических масштабах времени, наша планета ведет себя вообще как жидкое тело. Несложные расчеты показывают, что полюсное сжатие Земли, обусловленное ее быстрым осевым вращением, почти такое, как если бы Земля была жидким шаром. Другие примеры медленных течений в мантии: со скоростями несколько см/год расширяется знаменитый разлом Сан-Андреас в Калифорнии, расширяется дно океанов в рифтовых зонах срединно-океанических хребтов, относительно друг друга перемещаются материки, на несколько см в год поднимается Фенноскандия (послеледниковое поднятие) и т.д.
Рассмотрим простейшие положения реологии. Законы реологии эмпирические, как и ньютоновские законы механики. Каждый закон определяет реологическую модель тела.
Идеально упругое тело подчиняется закону Гука, согласно которому деформации (относительные изменения линейных и/или объемных размеров тела) пропорциональны приложенным напряжениям. Общая математическая формулировка закона Гука для однородного изотропного тела в тензорных обозначениях имеет вид:
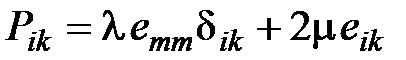 ,
,
где  – компоненты тензора напряжений (Н/м2),
– компоненты тензора напряжений (Н/м2), 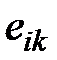 – компоненты тензора деформаций (безразмерны),
– компоненты тензора деформаций (безразмерны), 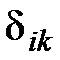 – символ Кронекера,
– символ Кронекера, 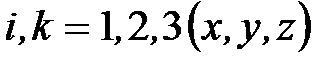 ,
, 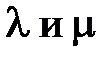 – упругие константы Ламэ (Н/м2). По повторяющемуся индексу m подразумевается суммирование.
– упругие константы Ламэ (Н/м2). По повторяющемуся индексу m подразумевается суммирование. 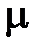 называют модулем сдвига (или жесткостью), а вместо
называют модулем сдвига (или жесткостью), а вместо 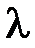 в геофизике чаще используют модуль всестороннего сжатия
в геофизике чаще используют модуль всестороннего сжатия 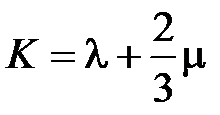 . Модуль сдвига (жесткость)
. Модуль сдвига (жесткость) 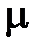 характеризует способность тела (среды) испытывать сдвиговые деформации, а модуль всестороннего сжатия характеризует способность тела (среды) изменять свой объем под действием внешних сил.
характеризует способность тела (среды) испытывать сдвиговые деформации, а модуль всестороннего сжатия характеризует способность тела (среды) изменять свой объем под действием внешних сил.
Далее для простоты будем рассматривать чисто сдвиговые деформации вдоль одной из осей координат (см. рис.).

|
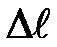
|
| P |
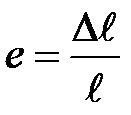
|
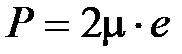 .
.
Для земной коры 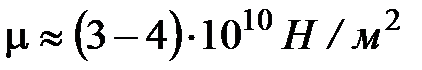 , для мантии
, для мантии 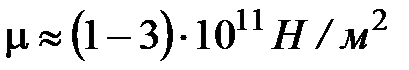 . Жесткость нижней мантии выше жесткости лучших сортов стали.
. Жесткость нижней мантии выше жесткости лучших сортов стали.
Другой предельной реологической моделью является модель вязкой ньютоновской жидкости:
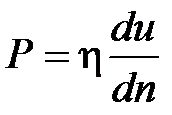 ,
,
где P – касательное напряжение, 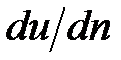 – производная от скорости по нормали к слоям,
– производная от скорости по нормали к слоям, 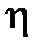 – коэффициент динамической вязкости (кг/(м с) = 10 г/(см с) = 10 Пуаз).
– коэффициент динамической вязкости (кг/(м с) = 10 г/(см с) = 10 Пуаз).
Модели идеально упругого тела и вязкой жидкости – это два предельных случая. Для упругого тела модуль сдвига отличен от нуля, для жидкости он равен нулю. Однако опыты показывают, что если через жидкость пропускать гиперзвуковые волны, то она начинает проявлять свойства твердого тела, в ней возникают и распространяются поперечные волны. При резком ударе о воду отклик будет как от твердой стенки. Получается, что поведение (реакция) среды зависит от продолжительности действия нагрузки.
Промежуточной реологической моделью, в которой среда обладает отличными от нуля и жесткостью (модулем сдвига), и вязкостью, является модель Максвелла (модель упруго-вязкого тела) с реологическим законом вида
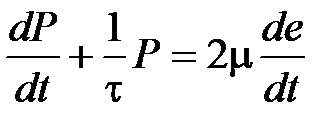 .
.
Здесь 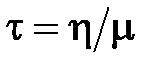 – постоянная, имеющая размерность времени. Ее физический смысл вытекает из следующих соображений. Предположим, что деформация с течением времени не изменяется, а нагрузка приложена. Тогда
– постоянная, имеющая размерность времени. Ее физический смысл вытекает из следующих соображений. Предположим, что деформация с течением времени не изменяется, а нагрузка приложена. Тогда
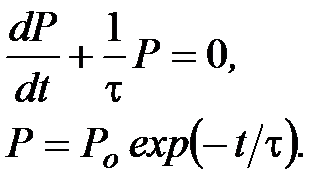
Таким образом, 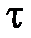 – это характерное время исчезновения приложенных напряжений (время релаксации). Легко видеть, что при
– это характерное время исчезновения приложенных напряжений (время релаксации). Легко видеть, что при 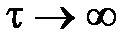 приходим к закону Гука (приложенные напряжения никогда не исчезают).
приходим к закону Гука (приложенные напряжения никогда не исчезают).
Реологическая модель Максвелла (модель наиболее часто используется при описании геотектонических процессов, хотя используются и другие реологические модели (Кельвина-Фойхта, Бингама и др.). Например, реологический закон для модели Кельвина-Фойхта (модель жестко-вязкого тела) имеет вид:
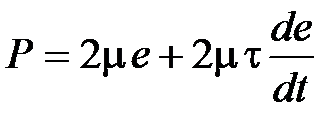 .
.
Здесь к закону Гука приходим при 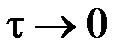 .
.
Механическими аналогами моделей Максвелла и Кельвина-Фойхта являются соответственно пружина и демпфер соединенные последовательно и параллельно.
Обе модели идеальные и поведение реальной Земли описывают приближенно. Важно то, что в этих моделях тело Земли и отдельные геооболочки рассматриваются как способные течь под действием приложенных в течение длительного времени нагрузок.
Вязкость обычных жидкостей порядка 10–2–102 Пуаз (вода – 10–2 Пуаз, глицерин – 40–50 Пуаз). Вязкость внутренних геооболочек имеет астрономические значения. По скорости послеледникового поднятия Фенноскандии оценили, что вязкость астеносферы порядка 1020 –1022 Пуаз, а вязкость нижней мантии по данным о сжатии Земли и того выше: порядка 1025–1026 Пуаз. Однако и при такой большой вязкости астеносфера для геодинамических процессов (типа вертикальные движения земной коры) с характерными временами порядка 104–105 лет ведет себя как текучее тело, а нижняя мантия ведет себя аналогично для процессов с характерными временами порядка 108 лет. Действительно, расширение дна океанов, относительные перемещения литосферных плит и другие проявления горизонтальных движений земной коры происходят со скоростями в несколько см в год и обусловлены, вероятнее всего, крупномасштабной конвекцией мантийного вещества. Если конвективная ячейка имеет характерные размеры порядка 2,9∙106 м, а скорость течения порядка 3 см/год, то характерное время порядка 108 лет как раз и получается.
Итак, для описания геодинамических процессов с малыми характерными временами (секунды, сутки) можно использовать модель Гука, с характерными временами в миллиарды лет – модель вязкой жидкости, а для описания процессов с характерными временами миллионы и сотни миллионов лет Землю следует рассматривать как тело Максвелла или тело Кельвина-Фойхта, или придумывать какие-нибудь другие более реальные модели.
| <== предыдущая страница | | | следующая страница ==> |
| Тепловой режим и температура в недрах Земли | | | Тирания Писистрата и Писистратидов. Реформы Клисфена |
Дата добавления: 2014-08-04; просмотров: 586; Нарушение авторских прав

Мы поможем в написании ваших работ!