Свойства оценок параметров модели

Условимся говорить о параметрах модели как о коэффициентах при варьируемых входных переменных. Тогда вычисление оценок параметров будет связано с данными о значениях входных и выходных переменных. Данные обычно представлены в виде статистики о наблюдаемом объекте.

Значение входных и выходных переменных являются случайными величинами с некоторым устоявшимся средним значением. Очевидно, и оценки параметров будут нести статистический, вероятностный характер.

Вероятность - это мера возможности события. Например, получение какой то величины измеряемой переменной носит вероятностный характер в силу действия различного рода помех, погрешности измерений, методических приближений, ошибок округления. Измеряемые переменные на некотором достаточно продолжительном времени позволяют собрать достаточную статистику, на основе которой можно получить средние значения. Эти средние значения оцениваются гипотетической вероятностью. Чем больше выборка, тем точнее оценивается среднее гипотетическое значение. Обычно предполагается, что статистика имеет нормальный закон распределения с математическим ожиданием М и дисперсией D. Также будем предполагать, что коэффициенты моделей могут быть определены методом наименьших квадратов (МНК).

Тогда для функции вида

.

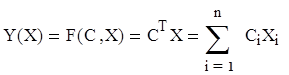используют метод наименьших квадратов:

,

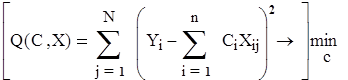где i=1,n, n-количество входных переменных,

j=1,N, N- количество экспериментов.

В результате применения метода наименьших квадратов получим следующие свойства оценок коэффициентов:

· Несмещенность. Оценки коэффициентов С являются несмещенными, если их математические ожидания при бесконечно большой выборке равны истинным значениям коэффициентов.

M[C] = C_ИСТ.

· Состоятельность. Оценки коэффициентов состоятельны, если они сходятся к истинным значениям коэффициентов по вероятности при величине выборки, стремящейся к бесконечности

lim P[(C_N –C_ИСТ)*(С_N -C_ИСТ)>e]=0.

N ¥

где Р – вероятность того, что разность между оценкой коэффициентов и истинным значением превысит наперед заданное положительное число e , равна нулю.

· Эффективность. Оценка коэффициентов эффективна, если среди ряда оценок эта оценка имеет минимальную дисперсию

D[С₀]<D[С₁].

Теория планирования экспериментов может обеспечивать одну или несколько характеристик оценок коэффициентов: несмещенность, состоятельность, эффективность.

Дата добавления: 2014-08-04; просмотров: 420; Нарушение авторских прав

Мы поможем в написании ваших работ!