
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Первое начало термодинамики для идеальных газов
Чтобы из общих термодинамических соотношений можно было получать конкретные результаты, надо знать, во-первых, уравнение состояния
f(P,V,T) = 0. (5.1)
Во-вторых, надо знать внутреннюю энергию тела как функцию параметров, определяющих его состояние, например
U = U(T,V). (5.2)
Выражение типа (5.2) называется калорическим уравнением состояния, в отличие от (5.1), называемого термическим уравнением состояния. Оба эти уравнения не могут быть получены методами теоретической термодинамики. Они находятся экспериментально, или методами статистической физики.
Рассмотрим приложения первого начала термодинамики к идеальным газам. Все слагаемые в уравнении первого начала термодинамики пропорциональны количеству вещества (числу молей n). Поэтому, чтобы не загромождать формулы, будем в дальнейшем рассматривать системы, состоящие из одного моля вещества.
Термическим уравнением состояния одного моля идеального газа является уравнение Клапейрона-Менделеева
PV = RT. (5.3)
Взяв дифференциал от обеих частей равенства (5.3) получим
PdV + VdP = RdT. (5.4)
Эксперименты показывают, что внутренняя энергия идеального газа не зависит от его объема, а является функцией только температуры. Такой вывод можно сделать на основании опытов по расширению газов в пустоту. В таком процессе внутренняя энергия не может измениться, т.к. газ не совершает работу и не получает тепло. Опыты показали, что температура газа не меняется, тогда как объем возрастает. Из этого можно сделать вывод, что при неизменной температуре внутренняя энергия идеального газа не зависит от объема. Иными словами, внутренняя энергия идеального газа является функцией только температуры U = U(T).
Функция U(T) может быть выражена через теплоемкость CV идеального газа. Выражение (4.4), справедливое для любого вещества, применительно к идеальному газу можно записать как
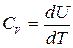 , или
, или 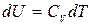 . (5.5)
. (5.5)
Отсюда следует, что теплоемкость CV идеального газа, как и его внутренняя энергия, не зависит от объема, а является функцией только температуры. Поэтому для идеального газа
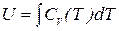 . (5.6)
. (5.6)
Опыт показывает, что во многих случаях CV в широких температурных интервалах (от 100 К до 1000 К) остается почти постоянной. Если пренебречь зависимостью CV от температуры, то вместо (5.6) можно использовать более простую формулу
U = CVT. (5.7)
Как показывают опыт и молекулярно-кинетическая теория, для одноатомных газов CV » 3R/2, для двухатомных CV » 5R/2, для многоатомных CV » 3R.
Рассмотрим теперь несколько важных частных случаев процессов с идеальными газами.
1) Изохорический процесс: V = const, dV = 0, C = CV.
dA = 0, dQ = dU = CV dT.
2) Изобарический процесс: P = const, dP = 0, С = СР.
Из соотношения (5.4), учитывая, что dP = 0, следует
dА = PdV = RdT.
Первое начало термодинамики (3.3) в этом случае примет вид
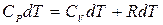 .
.
Сокращая на dT, получим 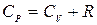 , или
, или
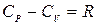 . (5.8)
. (5.8)
Это важное соотношение называется уравнением Роберта Майера.
Соотношение (5.8) может быть получено и из формулы (4.6), если учесть, что для идеального газа (¶U/¶V)T = 0, (¶V/¶T)P = R/P.
Работа А12 и количество тепла Q12 при изобарическом изменении объема от V1 до V2 равны
A12 = P(V2 – V1) = R(T2 - T1),
Q12 = CP(T2 – T1).
3) Изотермический процесс: Т = const, dT = 0.
dU = 0, dQ = dA = PdV.
При изотермическом расширении от объема V1 до объемаV2
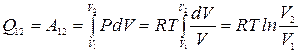 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Теплоемкость | | | Адиабатический процесс. Уравнение Пуассона |
Дата добавления: 2014-08-09; просмотров: 486; Нарушение авторских прав

Мы поможем в написании ваших работ!