Теорема Котельникова

3.1.Разложение непрерывных сигналов в ряд Котельникова

Телекоммуникационные сигналы делятся на непрерывные и дискретные.

Непрерывные сигналы (функции) могут принимать любые , сколь угодно близкие друг к другу значения, в любые моменты времени. Примером непрерывного сигнала является гармоническое колебание.

Дискретные (цифровые) сигналы могут принимать только заранее известные значения, отличающиеся одно от другого на конечную величину, причем изменяться эти значения могут только в определенные моменты времени. Примером дискретного сигнала является (см. рис.2.1 ) периодическая последовательность прямоугольных импульсов, которая в моменты времени ( -t/2 +кТ ) принимает значения или 0, или А.

Любая непрерывная функция, спектр которой не содержит частот

выше 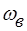, полностью определяется своими отсчетами, взятыми через интервал времени 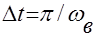. (Теорема Котельникова)

Временные диаграммы непрерывного сигнала x(t) и дискретизированного x _д(t) имеют вид:

x(t)

t

0 Dt 2Dt 3Dt 4DtРис. 3.1

x_д(t)

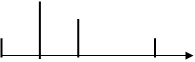0 Dt 2Dt 3Dt 4Dtt

Важно, что не надо передавать непрерывно исходный сигнал x(t),

достаточно передавать отсчёты x(kDt). Это первый шаг перехода от

непрерывного сигнала к цифровому. С точки зрения математики теорема Котельникова означает представление сигнала в виде ряда:

(3.1)

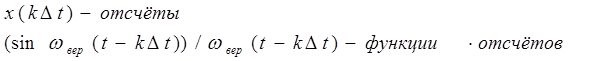Ряд Котельникова – это разложение сигнала 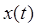в ряд по ортого-

нальным функциям .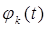

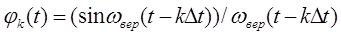(3.2)

Теоретически дискретизация осуществляется с помощью d-импульсов . Временная диаграмма одиночного d- импульса имеет вид:

u(t)

d(t-a)

Рис. 3.2 0 a t

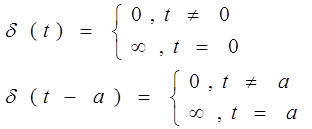
Спектр одиночного 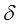- импульса получим, используя преобразование Фурье:

Использовано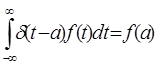
"фильтрующее" свойство дельта-функций:

Следовательно, спектр одиночного дельта-импульса имеет вид:

S(jw)

Рис. 3.3

w

Чтобы получить отсчёты функции 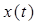перемножим функцию 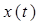на периодическую последовательность - импульсов с периодом Т=Dt. Временная диаграмма периодической последовательности дельта-импульсов имеет вид:

u_d(t)

d(t+4Dt) d(t+3Dt) d(t+2Dt) d(t+Dt) d(t) d(t-Dt) d(t-2Dt) d(t-3Dt)

. . . . . . .

-4Dt -3Dt -2Dt -Dt 0 Dt 2Dt 3Dt 4Dt t

Рис.3.4

Так как сигнал периодический, то его спектр будет дискретным.

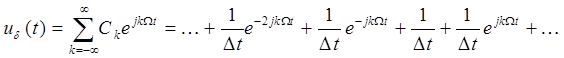
(3.3)

;

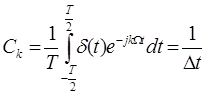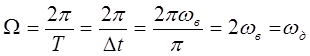
Т =D t ; 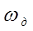-частота дискретизации.

Спектр периодической последовательности 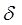- импульсов в соответствии с формулой для U(t) имеет следующий вид :

S(jw)

1/Dt Рис.3.5

. . . . . . . . . . .

t

--3w_д -2w_д -w_д 0 w_д 2w_д 3 w_д w

3.2. Спектр дискретизированного сигнала.

Рассмотрим временные диаграммы исходного и дискретизированного сигналов:

x(t)

t

Dt 2Dt 3Dt 4Dt Рис. 3.6

x_д(t)

0 Dt 2Dt 3Dt 4Dtt

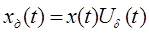-дискретизированный сигнал

- исходный сигнал.

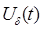-периодическая последовательность 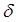- импульсов

Разложим периодическую последовательность d-импульсов в ряд Фурье, как мы это делали выше:

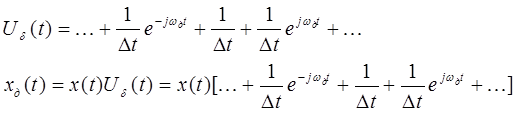
Найдём спектр дискретизированного сигнала.

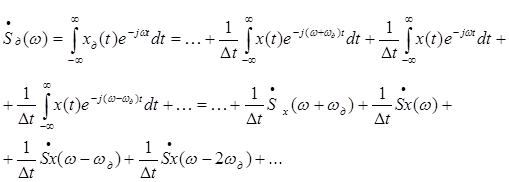(3.4)

Т.о. мы видим, что спектр дискретизированного сигнала содержит спектр исходного сигнала S_x(w), спектр исходного сигнала смещенный на величину частоты дискретизации вправо S_x(w - w_д), тот же спектр смещенный на величину частоты дискретизации влево S_x(w+ w_д), тот же спектр смещенный на величину 2w_д и т.д.

Спектр исходного непрерывного сигнала.

S_x(w)

Рис.3.8

-w_g w_g w

Спектр дискретизированного сигнала : _·

S_д(w)

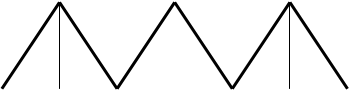Рис.3.9

……….. …………

(-w_д - w_в) - w _д - w_в 0 w_в w_д (w_д + w_в) w

3.3. Спектр дискретизированного сигнала при дискретизации импульсами конечной длительности (сигнал амплитудно-импульсной модуляции или АИМ сигнал).

Очевидно, что реально мы располагаем не последовательностью дельта-импульсов, а последовательностью импульсов конечной длительности.

В результате процесса дискретизации мы получим не последовательность дельта-импульсов, амплитуда которых соответствует значению непрерывного сигнала в тактовые моменты времени, а последовательность реальных, например, прямоугольных импульсов, амплитуда которых соответствует значениям непрерывного сингнала в тактовые моменты времени.

Рассмотрим временные диаграммы :

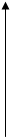
x(t) аналоговый сигнал

t

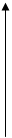U(t) периодическая последовательность импульсов

t

x_аим(t) сигнал АИМ

t

0 Dt 2Dt 3Dt 4Dt ……

Рис.3.10.

АИМ сигнал можно записать в виде:

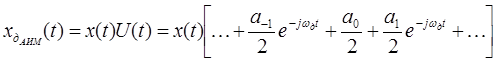
U(t)-периодическая последовательность импульсов.

В квадратных скобках – ряд Фурье для последовательности импульсов конечной длительности.

Спектр АИМ сигнала,следовательно, похож на спектр дискретизированного сигнала при дискретизации дельта -импульсами , но амплитуда составляющих спектра убывает с ростом номера гармоники : 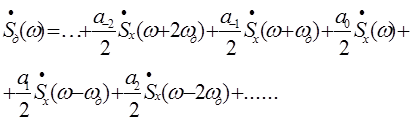(3.5)

Спектр АИМ сигнала в соответствии с формулой (3.5) принимает вид, показанный на рис.3.11.

_·

S_д(w)

-2w_д - w _д - w_в 0 w_в w_д 2w_д w

Рис.3.11

3.4. Восстановление непрерывного сигнала из отсчётов.

В линию связи передаются импульсы-отсчёты, которые поступают на вход приёмника.

Для восстановления исходного непрерывного сигнала из импульсов-отсчётов надо эти импульсы подать на вход идеального фильтра низких частот (ИФНЧ), который имеет следующие характеристики.

Амплитудно-частотная характеристика идеального ФНЧ (АЧХ ИФНЧ) имеет вид:

K(w)

K

- w_д 0 w_д w

Рис.3.12

Импульсная реакция ИФНЧ, т.е. реакция на дельта-импульс имеет вид:

g_ифнч (t)

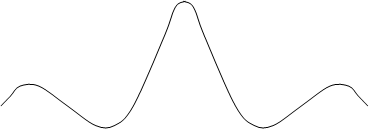Рис. 3.13

t

-3 Dt - 2Dt -Dt 0 Dt 2Dt 3Dt

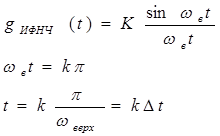(3.6)

Первая формула - это выражение для импульсной реакции ИФНЧ, вторая и третья формулы определяют моменты времени, для которых

g _ИФНЧ(t) обращается в ноль.

Cо спектральной точки зрения мы пропускаем дискретизированный сигнал, имеющий спектр в соответствии с рис.3.9 или 3.11, через ИФНЧ с АЧХ рис.3.12. Очевидно, что на выходе ИФНЧ получим спектр:

S(w)= K S_д(w) = K S_x(w) /Dt;

или для АИМ сигнала получим: S(w)= KS_д(w) = K a₀S_x(w) /2.

Таким образом, с точностью до постоянного множителя мы получили на выходе ИФНЧ спектр исходного сигнала x(t). С временной точки зрения мы получили исходный непрерывный сигнал x(t).

3.5. Погрешности дискретизации и восстановления непрерывных сигналов.

Теорема Котельникова точно справедлива только для сигналов с финитным (конечным) спектром. На рис.3.14 показаны некоторые варианты финитных спектров:

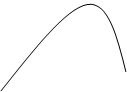
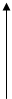S_x(w) 3

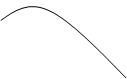2

1

0 w_в w

Рис.3.14.

Однако спектры реальных информационных сигналов бесконечны. В этом случае теорема Котельникова справедлива с погрешностью.

S_x(w)

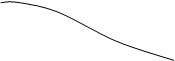
0 w_в w

Рис.3.15.

Погрешность дискретизации определяется энергией спектральных составляющих сигнала, лежащих за пределами частоты w_в.

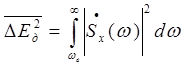(3.7)

Вторая причина возникновения погрешностей - неидеальность восстанавливающего ФНЧ.

Т.о. погрешность дискретизации и восстановления непрерывного сигнала определяется следующими причинами:

1) Спектры реальных сигналов не финитны.

2) АЧХ реальных ФНЧ неидеальны.

Например, если в качестве ФНЧ использовать RC- фильтр, то восстановленный сигнал на его выходе будет иметь вид:

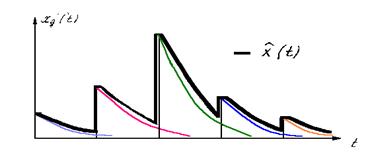
Рис.3.16.

с учетом того, что импульсная реакция RC-фильтра равна: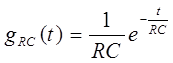

Вывод: чем выше 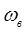и чем ближе характеристики ФНЧ к идеальным, тем ближе восстановленный сигнал к исходному.

Вопросы для самопроверки.

1. Какие сигналы называются непрерывными?

2.Какие сигналы называются дискретными?

3. Сформулируйте теорему Котельникова.

4.Рассчитайте и постройте спектр дискретизированного сигнала.

1. Рассчитайте и постройте спектр сигнала АИМ.

2. Как восстановить непрерывный сигнал из отсчетов?

3. Чем определяются погрешности дискретизации и восстановления сигналов?

Дата добавления: 2014-09-08; просмотров: 837; Нарушение авторских прав

Мы поможем в написании ваших работ!