Ортогональные проекции геометричЕских фигур

Как было показано ранее, проекцией точки при ортогональном проецировании называется основание перпендикуляра, опущенного из точки на плоскость проекций. Число, выражающее длинуэтого перпендикуляра от точки до ее проекции, называется координатой точки. Поэтому пространственная модель ортогонального проецирования точки на две или на три взаимно перпендикулярные плоскости проекций совпадает с прямоугольной системой декартовых координат.

В методе ортогонального проецирования положение точки определяется двумя проекциями (изображениями), а в методе прямоугольных координат тремя координатами (числами).

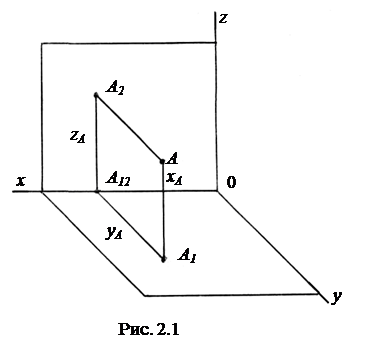Поместим начало координат в точке О на оси абсцисс x(рис. 2.1). Направим ось ординат yпо плоскости П₁, а ось аппликат z по плоскости П₂. Два пересекающихся проецирующих луча АА₁ и АА₂ определяют плоскость, перпендикулярную оси x. Эта плоскость пересекается с осью x в точке А₁₂ и с плоскостями П₁ и П₂ по прямым А₁А₁₂ и А₂А₁₂. При этом образуется прямоугольник координат АА₁А₁₂А₂. Тогда ОА₁₂=x_А; АА₁=А₂А₁₂=z_А; АА₂=А₁А₁₂=y_А, где z_А и y_А - соответственно координаты, определяющие расстояния от точки А до плоскостей проекций П₁ и П₂.

Дата добавления: 2014-09-26; просмотров: 416; Нарушение авторских прав

Мы поможем в написании ваших работ!