Интерпретация формул, содержащих кванторы

Логическое значение формул, содержащих кванторную приставку по переменной х, определяется для квантора существования $ как максимум из логических значений формулы, когда переменная кванторной приставки «пробегает» всю предметную область, и как минимум для квантора общности ", т.е.

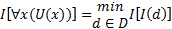
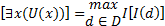
Здесь d - объект из предметной области, являющийся интерпретацией параметрического терма х, когда переменная x ²пробегает² предметную область. При определении логического значения формул логики предикатов необходимо учитывать следующие правила:

· вначале выполняются действия в скобках;

· кванторы связывают сильнее, чем отрицание, отрицание - сильнее, чем конъюнкция, конъюнкция - сильнее, чем дизъюнкция и импликация, последние - сильнее, чем эквивалентность.

Примеры

8. Найти логическое значение формулы 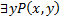в модели: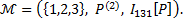

Формула является условием, так как переменная x входит в нее свободно. Следовательно, необходимо определить логическое значение формулы для каждого значения переменной x. Атом P двухместный. Таблица истинности для него содержит 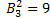строк (число размещений с повторениями из 3 по 2), а число различных функций интерпретации равно 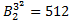. В заданной интерпретации 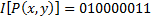. Операции по построению таблицы истинности формулы даны в табл. 6

Таблица 6 Интерпретация формул с логическими связками

x y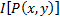

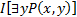
Переменная х свободна в данной формуле, поэтому значение формулы 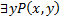с кванторной приставкой по переменной у определяется для каждого значения переменной x как максимум логических значений подформулы Р(х,у), когда переменная y пробегает всю предметную область.

9. Найти логическое значение формулы 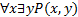в модели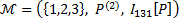

Последовательность действий по определению логического значения формулы очевидна из табл. 7.

Таблица 7 Интерпретация постоянной формулы

x y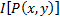

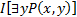
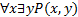
10. Составить таблицу истинности формулы 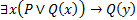в предметной области .

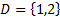Таблица истинности формулы языка логики предикатов в заданной предметной области содержит:

· все возможные наборы значений переменных, имеющих свободное вхождение в формулу,

· все возможные значения истинности атомных постоянных формул,

· все возможные функции интерпретации формул, содержащих свободные вхождения переменных и соответствующие этим интерпретациям истинностные значения всех подформул и самой формулы.

Переменная х входит в эту формулу связанно, а переменная y свободно. Следовательно, значение истинности всей формулы определяется значением переменной у в каждой возможной интерпретации атомов формулы Q(у) и Р.

Определим число строк таблицы истинности данной формулы. Переменные х и у пробегают предметную область

Так как функция интерпретации предикатных символов не указана, следует рассмотреть все возможные интерпретации формул Q(x,у) и Р. Из приведенных выше примеров очевидно, что в рассматриваемой модели атомная формула Q(х) может иметь четыре различных функции интерпретации, и длина каждой из этих функций равна двум. Постоянная атомная формула Р может иметь два истинностных значения: 0 и 1.

Таблица 8 Интерпретация параметрической формулы с кванторами

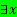
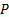
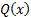
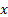
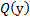
							y

Таким образом, подформула в области действия кванторной приставки может иметь 8 различных функций интерпретации, каждая из которых является двухэлементным вектором.

Общее число строк таблицы функций интерпретации каждой подформулы и формулы в целом при всевозможных сочетаниях логических значений ее подформул и переменных равно 16.

Последовательность действий при определении логического значения формулы очевидна из табл. 8.

11. Составить таблицу истинности формулы

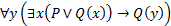
в модели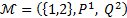

Построение таблицы истинности подформулы, находящейся в области действия квантора общности, показано в табл. 8, а таблицы истинности для всей формулы - в табл. 9.

Таблица 9 Интерпретация предложения, содержащего кванторы

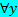
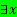
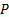
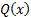
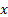
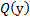
								y

Данный пример показывает, как значение функции интерпретации предложения зависит интерпретации всех предикатных символов, входящих в «большую» формулу.

12. Пусть предикат 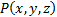означает .

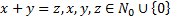Выясним, как влияет квантор на интерпретацию формулы. Очевидно, что 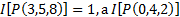=0. Сигнатура в данном случае содержит один функциональный символ (+) и один символ отношения .

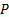Навесим теперь на предикат квантор существования: 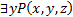содержит две свободные переменные и задает двухместный предикат, означающий 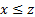. Вместо связанной переменной нельзя подставить конкретное значение, потому что логическое значение формулы оценивается по интерпретации бескванторной формулы на всей предметной области. При подстановке термов в формулу надо учитывать некоторые ограничения:

· вместо связанной переменной ничего подставлять нельзя. Ее можно только переименовать, используя для нового идентификатора переменной символ, который не встречается в «большой» формуле.

· Нужно следить за тем, чтобы при подстановке терма вместо свободной переменной в формуле не возникало новых связанных вхождений свободной переменной.

· Нужно также следить за тем, чтобы ни одна свободная переменная не оказалась в области действия квантора по связанной переменой.

· Несоблюдение этих правил приводит к искажению логического значение формулы в результате подстановок.

Постоянная формула, полученная навешиванием на параметрическую формулу квантора общности по всем свободно входящим переменным, называется 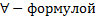или замыканием 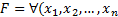P: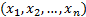

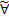)P = P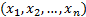

Постоянная формула, полученная навешиванием квантора 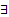по всем свободно входящим переменным, называется 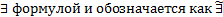(P).

Формула А называется общезначимой, если она истинна во всех моделях и во всех интерпретациях, т.е. в любой предметной области и в любой интерпретации. При этом замыкание А истинно, .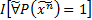

Формула 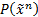выполнима, если она выполнима в какой-нибудь предметной области и в какой-нибудь интерпретации, т.е. если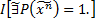

Формула А называется выполнимой, если она истинна в какой-либо интерпретации и в какой- Очевидно, что всякая общезначимая формула выполнима. Обратное не справедливо.

Пусть сигнатура содержит предикатный символ 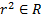в формуле 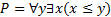. В модели 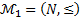формула P означает: существует наименьшее натуральное число, и она истинна. В то же время в модели 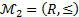формула F означает: существует наименьшее действительное число, и она ложна. Следовательно, указанная формула выполнима, но не общезначима.

Общезначимая формула А обозначается: 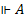. Например, .

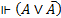Если формула А не выполнима ни в какой модели, т.е. ни в какой предметной области и ни в какой интерпретации, она называется противоречием. Например,. .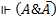

В бескванторных формулах вопрос о логическом значении формулы решается непосредственным использованием правил определения логического значения связок.

Для формул с кванторами процедура определения логического значения формулы осложняется тем, что предметные переменные имеют в общем случае бесконечные области определения. Поэтому прямой перебор всех значений невозможен и приходится использовать косвенные приемы, основанные на использовании правил интерпретации формул с кванторами.

Рассмотрим примеры.

Доказать общезначимость формулы

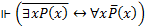
Пусть для некоторого предиката Р и предметной области D левая часть эквивалентности истинна. Тогда в предметной области не существует ни одного элемента 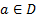, для которого 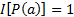. Следовательно, для всех 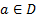формула 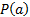ложна, а ее отрицание тождественно истинно. Согласно правилу интерпретации формул, образованных квантором общности, 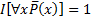. Таким образом, левая и правая части эквивалентности истинны, следовательно, формула истинна.

Пусть теперь левая часть эквивалентности ложна. Тогда в предметной области найдется хотя бы одно значение переменной х, равное а, при котором формула Р(а) истинна. Тогда для этого элемента предметной области отрицание формулы 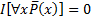будет ложно, и, следовательно, это доказывает, что рассматриваемая формула общезначима.

Доказать общезначимость формулы

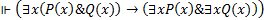
Если 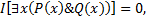то импликация истинна при любом логическом значении заключения импликации.

Если 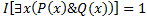, то импликация истинна только при истинном значении заключения импликации. Истинность посылки импликации в данном случае означает, что в предметной области найдется хотя бы один элемент 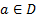, на котором обе формулы 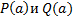истинны одновременно. Но в этом случае каждая из подформул, входящих в конъюнкцию в заключении импликации окажется истинной, и заключение импликации также будет истинно. В этом случае импликация также истинна.

Следовательно, данная формула общезначима.

Дата добавления: 2014-11-08; просмотров: 551; Нарушение авторских прав

Мы поможем в написании ваших работ!