
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Линейные разностные уравнения второго порядка
Определение 1.3. Линейным разностным уравнением второго порядка называется уравнение вида:
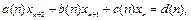 (1.7)
(1.7)
где 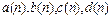 – заданные функции от n. Если
– заданные функции от n. Если 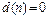 , то уравнение называется однородным. В противном случае
, то уравнение называется однородным. В противном случае 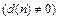 - не однородным.
- не однородным.
Если 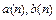 и
и 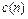 постоянные, то (1.7) называют уравнением с постоянными коэффициентами.
постоянные, то (1.7) называют уравнением с постоянными коэффициентами.
Уравнение (1.7) можно решить методами, аналогичными методам решения уравнений первого порядка. Полагая 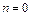 , можно выразить
, можно выразить 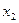 через
через 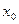 и
и 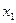 . Полагая
. Полагая 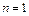 , выразим
, выразим 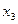 через
через 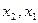 , а затем через
, а затем через 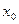 и
и 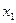 . Теоретически таким образом можно выразить
. Теоретически таким образом можно выразить 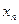 через
через 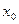 и
и 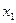 . Однако вычисления при этом оказываются очень громоздкими, и вывести общую формулу для
. Однако вычисления при этом оказываются очень громоздкими, и вывести общую формулу для 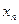 крайне трудно. Случай постоянных коэффициентов поддается решению общими методами.
крайне трудно. Случай постоянных коэффициентов поддается решению общими методами.
Рассмотрим линейное однородное разностное уравнение второго порядка с постоянными коэффициентами
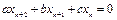 . (1.8)
. (1.8)
Будем считать 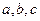 постоянными, причем
постоянными, причем 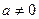 .
.
Будем искать решение уравнения (1.8) в виде:
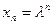 , (1.9)
, (1.9)
где 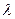 – некоторое число. Учитывая, что
– некоторое число. Учитывая, что 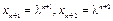 , из уравнения (1.8) получим:
, из уравнения (1.8) получим:
 ,
,
или, 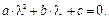 (1.10)
(1.10)
Уравнение (1.10) называется характеристическим уравнением для разностного уравнения (1.8). Оно является квадратным и имеет следующие корни:
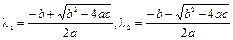 .
.
При решении характеристического уравнения следует рассматривать три случая. Два его корня могут быть действительными и различными (когда 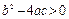 ); они могут быть действительными и равными между собой (
); они могут быть действительными и равными между собой (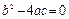 ) или же комплексными (
) или же комплексными (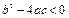 ).
).
Случай 1. Если  , то описанный выше метод дает два решения уравнения (1.8):
, то описанный выше метод дает два решения уравнения (1.8): 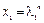 и
и 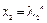 . Общее решение имеет вид:
. Общее решение имеет вид:
 , (1.11)
, (1.11)
где 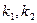 – произвольные постоянные.
– произвольные постоянные.
Постоянные 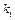 и
и 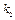 можно выразить через значения
можно выразить через значения 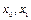 . Полагая
. Полагая 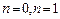 в решении (1.11) получаем:
в решении (1.11) получаем:
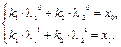
или
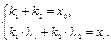
Решая систему уравнений, находим:
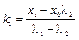 ,
, 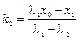 . (1.12)
. (1.12)
Таким образом, если даны 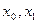 , то этим определено единственное решение уравнения (1.8).
, то этим определено единственное решение уравнения (1.8).
Пример 1.7. Найти общее решение разностного уравнения второго порядка 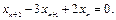 Выписать общую формулу для
Выписать общую формулу для 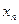 , если
, если 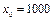 и
и 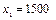 . Чему равно
. Чему равно 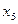 ?
?
Решение. Характеристическое уравнение 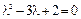 имеет корни
имеет корни
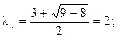
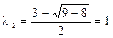 .
.
По формуле (1.11) общее решение имеет вид:
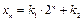 .
.
По формулам (1.12) находим:
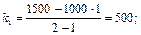
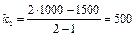 .
.
Таким образом, единственным решением, удовлетворяющим заданным начальным условиям, является
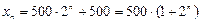 .
.
При 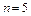 получаем
получаем 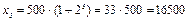 .
.
Случай 2. Если 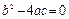 , то корни характеристического уравнения (1.10) равны между собой:
, то корни характеристического уравнения (1.10) равны между собой: 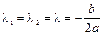 . Рассмотренный метод порождает лишь одно решение
. Рассмотренный метод порождает лишь одно решение 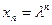 . Однако, другим решением уравнения (1.8) служит
. Однако, другим решением уравнения (1.8) служит 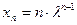 .
.
Тогда общее решение можно записать в виде:
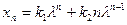 , (1.13)
, (1.13)
где 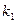 и
и 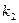 – произвольные постоянные. Чтобы убедиться в этом, подставим (1.13) в (1.8). Получим:
– произвольные постоянные. Чтобы убедиться в этом, подставим (1.13) в (1.8). Получим:
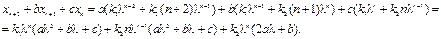
Первые два слагаемых обращаются в нуль, т.к. 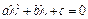 . Третье слагаемое равно нулю, поскольку
. Третье слагаемое равно нулю, поскольку 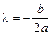 и
и 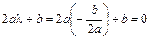 .
.
Итак, получим, что формула (1.13) дает общее решение уравнения (1.8).
Полагая 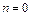 и
и 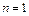 в (1.13), получим:
в (1.13), получим:
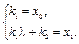
Отсюда, 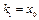 ,
, 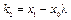 . (1.14)
. (1.14)
Пример 1.8. Найти общее решение разностного уравнения второго порядка 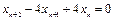 . Найти
. Найти 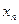 , если
, если 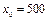 и
и 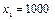 .
.
Решение. Характеристическое уравнение 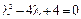 имеет единственный корень
имеет единственный корень 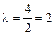 . Поэтому общее решение уравнения имеет вид:
. Поэтому общее решение уравнения имеет вид:
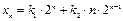 .
.
Полагая 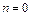 ,
, 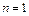 , получаем
, получаем 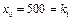 и
и 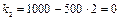 . Таким образом,
. Таким образом, 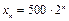 . В частности,
. В частности, 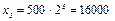 .
.
Случай 3. Если 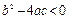 , то корни характеристического уравнения (1.10) являются комплексно-сопряженными числами:
, то корни характеристического уравнения (1.10) являются комплексно-сопряженными числами:
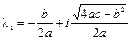 ,
, 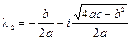 , (1.15)
, (1.15)
где 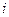 – мнимая единица
– мнимая единица 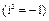 .
.
Общее решение уравнения (1.8) записывается в виде:
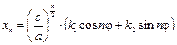 , (1.16)
, (1.16)
где 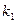 ,
, 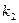 – произвольные постоянные,
– произвольные постоянные, 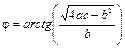 .
.
Постоянные 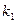 ,
, 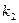 можно выразить, как и прежде, через
можно выразить, как и прежде, через 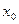 и
и 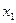 .
.
Решение (1.16) разностного уравнения (1.8) обладает интересными свойствами. Так как 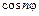 и
и 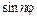 с увеличением
с увеличением  колеблются между значениями -1 и 1, решение
колеблются между значениями -1 и 1, решение 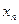 также колеблется несколько более сложным образом. Свойство этого решения покажем на примере.
также колеблется несколько более сложным образом. Свойство этого решения покажем на примере.
Пример 1.9. Найти общее решение разностного уравнения второго порядка 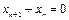 . Найти
. Найти 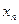 , если
, если 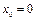 , а
, а 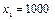 .
.
Решение. Характеристическое уравнение 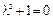 имеет комплексные корни
имеет комплексные корни 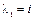 ,
, 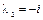 . Так как
. Так как 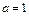 ,
, 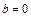 ,
, 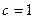 , то
, то 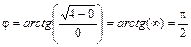 . Отсюда общее решение
. Отсюда общее решение
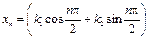 .
.
Полагая 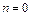 и
и  , получаем
, получаем 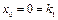 и
и 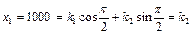 . Искомое решение есть
. Искомое решение есть
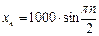 .
.
В частности, 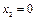 ,
, 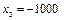 ,
, 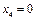 ,
, 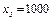 и т.д.
и т.д.
Пример 1.10. С целью анализа распространения инфекционных заболеваний в школе ведется запись вспышек кори. Согласно полученным оценкам, вероятность 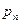 возникновения хотя бы одного нового случая заболевания спустя
возникновения хотя бы одного нового случая заболевания спустя  недель после вспышки удовлетворяет уравнению
недель после вспышки удовлетворяет уравнению 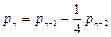 . Найдите
. Найдите 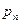 , если
, если 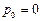 и
и 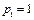 .
.
Решение. Характеристическое уравнение 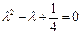 имеет корни
имеет корни 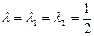 . Учитывая формулу (1.13), получим:
. Учитывая формулу (1.13), получим:
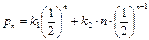 .
.
Считая 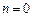 и
и 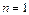 , имеем:
, имеем:
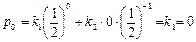 .
.
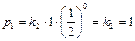 .
.
Искомое решение есть
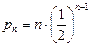 . (1.17)
. (1.17)
Из (1.17) последовательно находим: 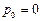 ,
, 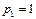 ,
, 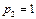 ,
, 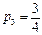 ,
, 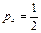 . Отсюда заключаем, что через три недели вероятность нового случая кори становится меньше 50 %.
. Отсюда заключаем, что через три недели вероятность нового случая кори становится меньше 50 %.
1.3. Метод вариации постоянных для разностных уравнений второго порядка
Рассмотрим линейное неоднородное разностное уравнение второго порядка с постоянными коэффициентами
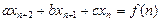 , (1.18)
, (1.18)
с постоянными 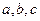 (при
(при 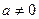 ).
).
Для решения уравнения (1.18) применим методы, использованные в
п. 1.2, но для простоты рассмотрим лишь случай действительных и различных корней 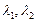 .
.
Пусть 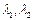 – корни характеристического уравнения
– корни характеристического уравнения 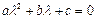 , соответствующего однородному уравнению (1.8). Тогда
, соответствующего однородному уравнению (1.8). Тогда 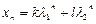 – общее решение (1.8), причем
– общее решение (1.8), причем 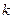 и
и 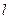 – произвольные постоянные.
– произвольные постоянные.
Идея метода вариации постоянных состоит в том, чтобы считать постоянные 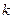 и
и 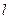 зависящими от
зависящими от  таким образом, что получается решение неоднородного уравнения (1.18). Согласно этому, будем искать решение в виде:
таким образом, что получается решение неоднородного уравнения (1.18). Согласно этому, будем искать решение в виде:
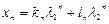 , (1.19)
, (1.19)
где 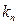 и
и 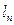 могут изменяться вместе с
могут изменяться вместе с  .
.
Из (1.19) имеем:
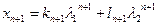 .
.
Прибавив к правой части и отняв от нее величину 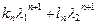 , получим:
, получим:
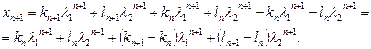
Для упрощения записи будем считать, что
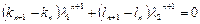 , (1.20)
, (1.20)
при любом значении  . Тогда получим:
. Тогда получим:
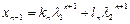 . (1.21)
. (1.21)
Из уравнения (1.21) имеем: 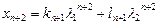 . Поступая как и выше, получим:
. Поступая как и выше, получим:
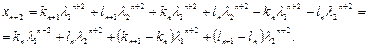 (1.22)
(1.22)
Подставив теперь выражения (1.22), (1.21), (1.19) в уравнение (1.18), получим:
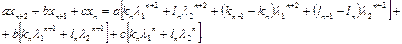
Группируя слагаемые и приравнивая правую часть 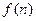 ,имеем:
,имеем:
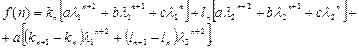 (1.23)
(1.23)
Т.к. 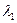 и
и  – корни характеристического уравнения, то первые два выражения в квадратных скобках (1.23) обращаются в нуль и, значит,
– корни характеристического уравнения, то первые два выражения в квадратных скобках (1.23) обращаются в нуль и, значит,
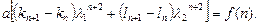 (1.24)
(1.24)
Объединив (1.20) и (1.24), мы получим систему двух уравнений
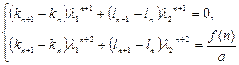 (1.25)
(1.25)
относительно двух неизвестных 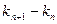 и
и 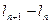 .
.
Решив систему, получим:
 , (1.26)
, (1.26)
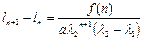 . (1.27)
. (1.27)
Уравнения (1.26) и (1.27) представляют собой линейные разностные уравнения первого порядка, которые можно решить методами п.1.1.
Решая (1.26), получаем:
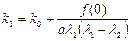 ,
,
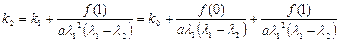 ,
,
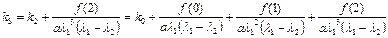 ,
,
…
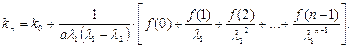 (1.28)
(1.28)
Аналогично для уравнения (1.27) имеем общее решение
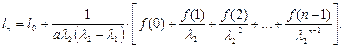 (1.29)
(1.29)
Т.о., общее решение уравнения (1.18) запишется в виде
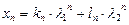 , (1.30)
, (1.30)
где 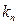 и
и 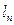 выражаются формулами (1.28), (1.29).
выражаются формулами (1.28), (1.29).
Если известны 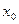 и
и 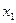 , то постоянные
, то постоянные 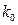 и
и 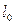 находим из уравнений
находим из уравнений 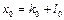 ,
, 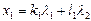 .
.
Пример 1.11. Если бы популяция рыб росла, не подвергаясь внешним возмущениям, то ее прирост в 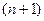 -м году был бы вдвое больше прироста в
-м году был бы вдвое больше прироста в  -м году. Однако в исследовательских целях к популяции ежегодно добавлялось по 100 рыб. Найти
-м году. Однако в исследовательских целях к популяции ежегодно добавлялось по 100 рыб. Найти 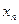 – численность популяции рыб в
– численность популяции рыб в  -м году, если
-м году, если 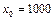 ,
, 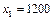 .
.
Решение. Численность рыб 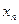 удовлетворяет разностному уравнению второго порядка
удовлетворяет разностному уравнению второго порядка 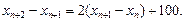
Или 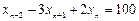 .
.
Здесь 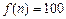 . Характеристическим служит уравнение
. Характеристическим служит уравнение 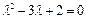 с корнями
с корнями 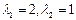 . Общее решение уравнения имеет вид:
. Общее решение уравнения имеет вид:
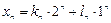 .
.
По формулам (1.28), (1.29) находим:
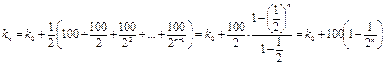 .
.
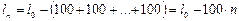 .
.
Таким образом,  .
.
Найдем постоянные 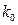 и
и 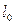 . При
. При  и
и 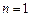 имеем:
имеем:
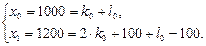
Отсюда 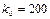 ,
, 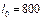 , а искомое решение есть
, а искомое решение есть
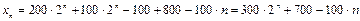 .
.
В частности, 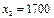 ,
,  ,
, 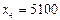 . Ясно, что численность рыб продолжает очень быстро возрастать.
. Ясно, что численность рыб продолжает очень быстро возрастать.
| <== предыдущая страница | | | следующая страница ==> |
| Линейные разностные уравнения первого порядка | | | Лекция 3. Дифференциальные уравнения |
Дата добавления: 2014-03-11; просмотров: 834; Нарушение авторских прав

Мы поможем в написании ваших работ!