Уравнение Клапейрона–Клаузиуса

Ограничимся рассмотрением фазовых переходов первого рода, для которых характерно равенство изобарно-изотермических потенциалов двух фаз и скачкообразное изменение энтропии S и объёма V.

Будем рассматривать равновесие чистого вещества в двух фазах однокомпонентной системы (k = 1). Это могут быть следующие процессы:

а) А_тв 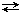А_ж – это процесс плавления (обратный процесс – кристаллизация);

б) А_ж 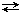А_газ – процесс испарения (обратный процесс – конденсация);

в) А_тв 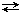А_газ – процесс сублимации (возгонки), (обратный процесс – десублимация или конденсация);

г) А_тв,a 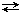А_тв,b – переход твердого тела из одной полиморфной (аллотропной) модификации в другую.

Для равновесия двух фаз (1) и (2) чистого вещества должны выполняться следующие условия:

р⁽¹⁾ = р⁽²⁾; (1)

Т⁽¹⁾ = Т⁽²⁾; (2)

m⁽¹⁾ = m⁽²⁾; (3)

Из соотношения (3)получим, что dm⁽¹⁾ = dm⁽²⁾ (4)

Но для чистого вещества химический потенциал m есть ни что иное, как молярная энергия Гиббса: .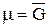

Поэтому .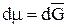

Но .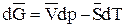

Для двух фаз (1) и (2) соотношение (4) примет вид:

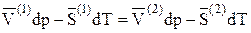(5)

Перегруппируем члены:

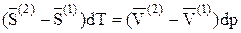, откуда

.

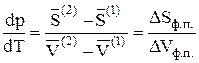Таким образом, получаем:

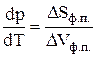(6)

Соотношения (6) – это одна из форм записи уравнения Клапейрона-Клаузиуса.

Здесь DS_ф.п. – молярная энтропия фазового перехода (т.е. разность молярных энтропий вещества в двух фазах);

DV_ф.п. – разность молярных объемов вещества в двух фазах.

Если рассматривать обратимые изотермические фазовые переходы, то для них

.

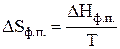Тогда уравнения (6) можно переписать в следующем виде:

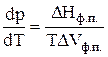(7)

Соотношение (7) – это тоже уравнение Клапейрона–Клаузиуса. Здесь Т – температура фазового перехода, DН_{ф.п .} – молярная теплота (энтальпия)

фазового перехода. Величину 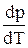часто называют температурным коэффициентом давления насыщенного пара. Величина 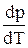является угловым коэффициентом соответствующих кривых р = р(Т) (сублимации, испарения, плавления и полиморфных превращений).

Рассмотрим вначале равновесия с участием пара.

а) твердое вещество 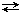пар – возгонка (сублимация);

б) жидкость 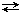пар – испарение (конденсация).

Если рассматривать равновесия в области температур, далеких от критической, то можно записать:

;

,

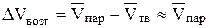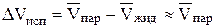поскольку объемом конденсированной фазы по сравнению с объемом пара можно пренебречь. Считая, что пар подчиняется законам идеальных газов

для 1 моль газа имеем:

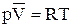и ,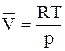

тогда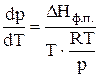

откуда следует, что 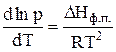(8)

Соотношение (8)–дифференциальная форма уравнения Клапейрона-Клаузиуса для процессов возгонки или испарения.

Так как DH_возг > 0 и DH_исп > 0, то lnp (а, значит, и р) – возрастающая функция, т.е. давление насыщенного пара над веществом увеличивается при увеличении температуры.

Разделим переменные в соотношении (8) Считаем, что в узком температурном интервале DH_ф.п. = const.

1) Возьмем неопределенный интеграл:

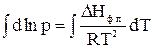
Отсюда:

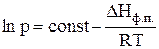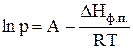или (9)

Уравнение прямой в координатах ln p-1/Т.

DН_возг > DН_испар,

Поэтому кривая возгонки р = р(Т) должна идти круче, чем кривая испарения. Если на одном графике изобразить зависимости в координатах lnp=f ( 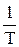), то будет наблюдаться следующая картина:

Линия АВ - соответствует процессу испарения, а линия ВС - процессу возгонки.

2) Возьмем определенный интеграл:

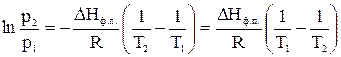(10)

Рассмотрим теперь процесс плавления:

Воспользуемся уравнением Клапейрона-Клаузиуса в виде:

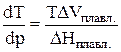(11)

Здесь Т – температура плавления;

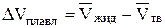; DН_плавл – молярная теплота плавления.

Знак производной 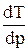зависит от знака DV_плавл. Обычно 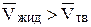_, поэтому

DV_плавл > 0. Есть несколько исключений (например, вода, висмут, галлий для которых DV_плавл < 0).

Температура фазового перехода между конденсированными фазами слабо зависит от давления р, поэтому соотношение (11) можно переписать в виде:

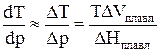
Пример 4.4Как изменится температура плавления льда с изменением внешнего давления, если Δ_плН = 79,7 кал/г при t = 0 ^оС, а удельные объемы воды и льда при этой температуре равны соответственно: V_ж = 1,0001 см³/г и V_лед = 1,0908 см³/г.

Решение.Воспользуемся уравнением Клаузиуса – Клапейрона в виде (4.16)

.

,

.

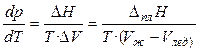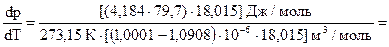
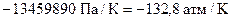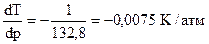Пример 4.5Как изменится температура кипения воды с ростом давления, если при температуре t = 100 ^оС Δ_испН = 539,7 кал/г, V_пар = 1651 см³/г, V_ж = 1 см³/г.

Дата добавления: 2014-05-02; просмотров: 719; Нарушение авторских прав

Мы поможем в написании ваших работ!