
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
РАЗЛИЧНЫЕ ФОРМЫ ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ
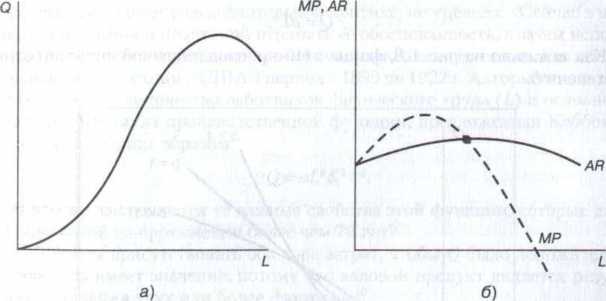
1. производственная функция начинается с увеличения маржинальной отдачи, после чего следует уменьшение маржинальной отдачи. Иными словами, присутствуют все три стадии производства. Эта ситуация представлена кубической функцией:
Q = a +bL + cL2-dL3,
где а является константой, а Ь, с и d являются коэффициентами.
|
2. Квадратичной функции уменьшение маржинальной отдачи, а не первую стадию производства:
Q = а + bL – cL2.
| Q |
| AP |
| MP |
3. Линейную производственную функцию Q = a + bL. Эта функция не демонстрирует уменьшающейся отдачи; валовой продукт будет прямой линией с наклоном Ь, а линии МР и АР будут горизонтальными и совпадающими.
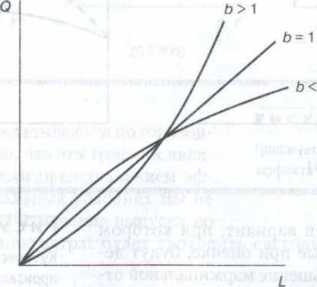
4. Показательная функция, которая имеет следующий вид:
Q = aLb.
форма этой производственной функции зависит от степени b;.
|
ПРОИЗВОДСТВЕННАЯ ФУНКЦИЯ КОББА—ДУГЛАСА
Q=aLbKс.
Широко использовалась как для оценки производственных функций отдельных фирм, так и для оценки совокупных производственных функций.
Свойства этой функции:
1. Должны присутствовать оба типа затрат, чтобы Q было положительным числом. Это имеет значение, потому что валовой продукт является результатом объединения двух или более факторов.
2. Функция может демонстрировать увеличивающуюся, уменьшающуюся и постоянную отдачу.
3. При такой структуре, если b + с > 1, отдача увеличивается, а если b + с < 1, отдача уменьшается.11 Если b + с = 1, отдача является постоянной.
4. Функция позволяет нам исследовать влияние любого фактора на маржинальный продукт, оставляя при этом остальные факторы неизменными. Следовательно, она полезна при анализе производственной функции в краткосрочном периоде.
маржинальный продукт труда оказывается равным MPL = bQ/L,
маржинальный продукт капитала равняется МРК = cQ/K.
Каждый коэффициент всегда будет меньше 1, и это будет означать, что каждый демонстрирует уменьшающуюся маржинальную отдачу. Таким образом, производство находится на стадии II, которая является важной областью производства.
5. Так как показательную функцию можно преобразовать в линейную, используя логарифмы, ее можно оценить при помощи линейного регрессионного анализа. Это можно сделать с помощью достаточно простых вычислений, используя любой пакет программ.
6. Хотя мы свели наше обсуждение всего лишь к двум переменным затратам (L и К), функция Кобба—Дугласа может вмещать в себя любое число независимых переменных:
Q = a 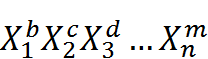
СТАТИСТИЧЕСКАЯ ОЦЕНКА ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ
Где взять данные?
Когда статистическая оценка касается предприятия или группы предприятий, данные берутся из документов компании — бухгалтерских, кадровых, платежных, производственных и др.
Измерение объема.
Если на предприятии производится только один продукт, Q устанавливается в физических единицах (например, штуках, тоннах, галлонах).
Если предприятие производит несколько различных продуктов, возможно, придется зафиксировать определенную меру ценности, присваивая продуктам весовые коэффициенты в зависимости от создаваемой ценности (например, на основе издержек или отпускной цены).
Измерение затрат.
Затраты должны измеряться как «поточные», а не «ресурсные» переменные (например, количество часов труда, а не количество работников)
Для материалов лучше всего подходят физические показатели (например, вес потребляемых материалов).
Можно посоветовать использовать только наиболее важные сырьевые материалы.
В качестве альтернативы можно использовать сочетание материалов (но весу или ценности).
Наиболее сложной переменной являются крайне важные затраты капитала. В некоторых случаях показателем использования капитала могут служить периодические амортизационные отчисления.
Проблемы:
· амортизационные отчисления, записанные в бухгалтерских документах компании, часто основываются на бухгалтерских правилах или требованиях закона.
· прогнозируемый срок амортизации механизма чаще всего зависит от принципов налогообложения, потому что в целях налогообложения фирма стремится воспользоваться списанием как можно раньше.
· Некоторые виды капитала, например земля, не подлежат амортизации.
Числовой пример производственной функции Кобба- Дугласа
Была отобрана группа панельных данных по двенадцати заводам, занимающихся розливом прохладительных напитков. Данные относятся к определенному месяцу в 1998 г.
Используются только две независимые переменные:
1. количество работников, задействованных в непосредственном производстве,
2. размер завода.
Производство, зависимая переменная, выражена в галлонах продукта, отгруженного за рассматриваемый период.
Производственная функция: розлив прохладительных напитков
| Валовой продукт | Труд | Капитал |
| 1.00 | ||
| 1,00 | ||
| 1,00 | ||
| 1.00 | ||
| 1,25 | ||
| 1,25 | ||
| 1,25 | ||
| 1.25 | ||
| 1,25 | ||
| 1,50 | ||
| 1,50 | ||
| 1,50 | ||
| 1,50 | ||
| 1,50 | ||
| 1,50 | ||
| 1.75 | ||
| 1,75 | ||
| 1,75 | ||
| 1,75 | ||
| 1,75 |
Статистика регрессии
| R-квадрат | 0,980965846 | ||
| Скорректированный R-квадрат | 0,978726534 | ||
| Стандартная ошибка | 0,020818585 | ||
| Наблюдения | |||
| Коэффициенты | Стандартная ошибка | tстатистика | |
| Пересечение | 1,1800154 | 0.096022924 | 12.288892 |
| X Переменная 1 | 0,6643702 | 0,075371367 | 8.8146228 |
| X Переменная 2 | 0,3214714 | 0,147006777 | 2.1867796 |
К числам была применена формула функции Кобба—Дугласа — Q = nLbKc
Результаты регрессии выглядят следующим образом:
Q = 15,14L0,66K0,32
| <== предыдущая страница | | | следующая страница ==> |
| Управленческая экономика. Теория производства | | | РАСПРОСТРАНЕНИЕ ОИ В АТМОСФЕРЕ (А) |
Дата добавления: 2014-05-17; просмотров: 365; Нарушение авторских прав

Мы поможем в написании ваших работ!