Резонансный интеграл

Пусть мы имеем однородную бесконечную среду – смесь резонансного поглотителя с концентрацией 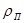и сечением потенциального рассеяния s_p и замедлителя с концентрацией 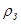и сечением рассеяния s_s. Полное сечение потенциального рассеяния для такой однородной среды

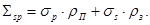(15)

Рассмотрим резонансное поглощение нейтронов при замедлении на примере единичного изолированного резонансного уровня при энергии .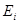

Введем следующие параметры резонансов:

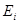– энергия резонансного уровня;

s_0i – сечение в центре резонансной линии при E_i ;

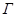– ширина резонанса;

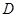– расстояние между резонансами.

– эффективная ширина резонанса, то есть область энергий, где еще учитывается воздействие резонанса на спектр нейтронов. Если 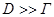, то резонанс можно считать изолированным.

Для одиночного изолированного резонанса справедлива формула Брейта-Вигнера

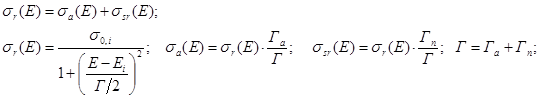(16)

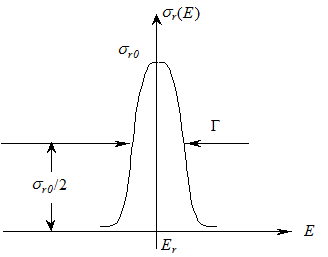
Рис. 2. Резонансная линия Брейта-Вигнера .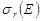

E_r – точка максимума резонанса

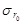- амплитуда резонансной линии

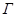– ширина резонанса на его полувысоте.

Как известно, в случае слабого поглощения среды поток нейтронов в ней описывается возрастным приближением, а вероятность избежать резонансного поглощения в возрастном приближении имеет вид

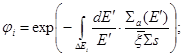(17)

где

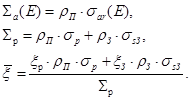(18)

Сечение потенциального рассеяния поглотителя и замедлителя слабо меняются в пределах резонансного уровня, поэтому величину 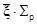можно вынести из под знака интеграла. В результате получим следующее выражение

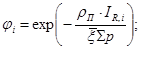(19)

где

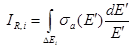(20)

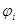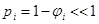носит название резонансного интеграла. Заметим, что для одного резонансного уровня ~1 и , где 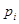– есть вероятность нейтрону испытать поглощение на i-ом резонансе. Поэтому ,

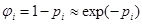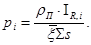(21)

Вычислим резонансный интеграл для одиночного резонансного уровня

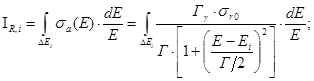(22)

Если область действия резонанса 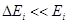, то переменную 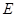в знаменателе подынтегрального выражения можно вынести из под знака интеграла, присвоив ей значение резонансной энергии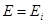

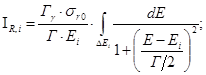(24)

Производя стандартную замену переменных интегрирования

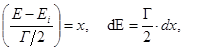
резонансный интеграл представим в виде

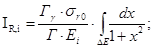(25)

Пределы интегрирования по переменной 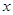симметричны относительно 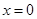. Наибольшее значение подынтегральное выражение принимает в центре резонансной линии 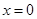, и при энергиях, отличных от резонансной энергии, это выражение стремиться к нулю. Поэтому пределы интегрирования можно распространить от -¥ до +¥, так как основное значение интеграл набирает в области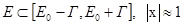

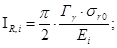(26)

Однако, если концентрация резонансного поглотителя достаточно велика, поглощение в резонансе становится существенной величиной и поток нейтронов в районе резонанса сильно изменяется с энергией, поэтому возрастное приближение становится неприменимым для этого случая.

Дата добавления: 2014-08-09; просмотров: 793; Нарушение авторских прав

Мы поможем в написании ваших работ!