
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
НЕПРЕРЫВНО – ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ
Рассмотрим особенности непрерывно-детерминированного подхода на примере использования в качестве математических моделей дифференциальных уравнений.
В непрерывно-детерминированных моделях случайные факторы не учитываются. Время 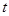 непрерывно, недескретизированно.
непрерывно, недескретизированно.
Детерминированные уравнения, - в которых неизвестными были функции одной или нескольких переменных, причем в уравнения входят не только функции, но и их производные различных порядков.
Если неизвестные функции многих переменных, то уравнения называются в частных производных.
Если независимая переменная – одна, то ОДУ.
Если независимая переменная – время 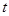 , то математическое соотношение в общем виде:
, то математическое соотношение в общем виде:
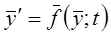 ;
; 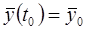 ,
,
где 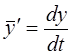 ;
; 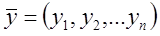 , n – мерные векторы ®
, n – мерные векторы ® 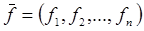
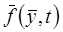 - вектор функция, которая определена на некотором
- вектор функция, которая определена на некотором  - мерном
- мерном 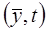 множестве и является непрерывной.
множестве и является непрерывной.
Так как математические схемы такого вида отражают динамику изучаемой системы, то они и называются 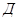 - схемы, т.е. динамическими.
- схемы, т.е. динамическими.
В простейших случаях 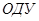 - записывается:
- записывается:
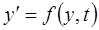
Наиболее важно для системотехники приложение 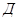 - схем в ТАУ.
- схем в ТАУ.
Рассмотрим в качестве примера две колебательные системы:
1. механическую 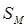 - маятник.
- маятник.
2. электронную 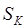 - колебательный контур.
- колебательный контур.
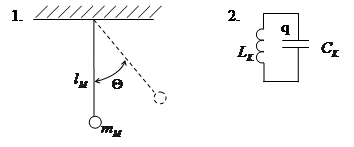

1) ОДУ: 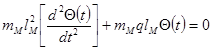
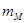 - масса маятника
- масса маятника
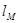 - длина маятника
- длина маятника
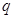 - ускорение свободного падения
- ускорение свободного падения
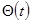 - угол
- угол
отсюда можно найти необходимые характеристики, например период 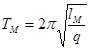
2) ОДУ: 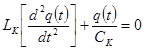
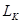 - индуктивность контура
- индуктивность контура
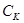 - емкость контура
- емкость контура
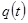 - заряд в момент времени
- заряд в момент времени 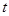
отсюда 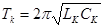 - период
- период
Введём обозначение:
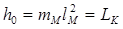 ;
; 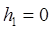 ;
; 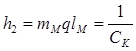 ;
; 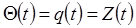
Т.е. получим ОДУ второго порядка, описывающего поведение этой замкнутой системы:
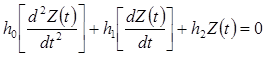
где 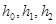 - параметры системы
- параметры системы
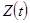 - состояние системы в момент времени
- состояние системы в момент времени 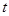 ; т.е. поведение обоих объектов может быть исследовано на основе одной математической модели, к тому же они взаимозаменяемы.
; т.е. поведение обоих объектов может быть исследовано на основе одной математической модели, к тому же они взаимозаменяемы.
Если излучаемая система 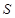 взаимодействует с внешней средой
взаимодействует с внешней средой 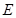 , то появляется входное воздействие
, то появляется входное воздействие 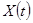 (внешняя сила для
(внешняя сила для 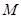 , или источник энергии для
, или источник энергии для 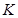 ) и математическая модель имеет вид:
) и математическая модель имеет вид:
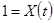
Получаем, что 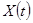 - входная, а
- входная, а 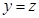 - выходная переменная системы в момент
- выходная переменная системы в момент 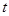 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Глубина моделирования | | | СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ |
Дата добавления: 2014-08-09; просмотров: 385; Нарушение авторских прав

Мы поможем в написании ваших работ!