
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
АВТОМАТИЗАЦИЯ МЕТАЛЛУРГИЧЕСКОГО ПРОИЗВОДСТВА
Методические указания к практическим занятиям, лабораторным работам и СРМП Расчетная работа №4
4 АППРОКСИМАЦИЯ КРИВОЙ РАЗГОНА И РАСЧЕТ НАСТРОЕЧНЫХ ПАРАМЕТРОВ РЕГУЛЯТОРОВ
Нужно выполнить следующие задания:
1) выполнить аппроксимацию кривой разгона по методу касательной;
2) выполнить аппроксимацию кривой разгона методом Симою;
3) вычислить настроечные параметры П и ПИ регуляторов.
1 Выдержка из лекций
По аппроксимации кривой разгона.
Существуют два основных метода определения характеристик объекта управления: аналитический и экспериментальный.
В практике автоматического регулирования наибольшее распространение нашел экспериментальный метод. Экспериментальный метод включает в себя три этапа:
- экспериментальное снятие кривой разгона на реальном объекте;
- назначение вида передаточной функции;
- определение параметров этой передаточной функции.
Снятие кривой разгона предусматривает ступенчатое изменение входного воздействия и наблюдение выходной переменной объекта. При снятии кривой разгона очень важно, чтобы перед нанесением ступенчатого воздействия объект находился в стационарном режиме, после воздействия он также должен прийти в установившееся положение.
Величина ступеньки должна быть достаточно большой, чтобы уверенно зафиксировать изменение выходной переменной на фоне помех, в то же время слишком большая ступенька может нарушить нормальный ход технологического процесса. Компромиссный вариант выбирается опытным путем.
В практике автоматического регулирования вид передаточной функции определяется выбором из ограниченного числа структур. Мы рассмотрим два вида, нашедшие наибольшее применение в металлургии и теплотехнике.
1) Объект представлен дифференциальным уравнением первого порядка с запаздыванием. Его передаточная функция – это последовательно соединенные апериодическое звено и звена запаздывания и имеет вид
 |
где kоб - коэффициент передачи объекта;
Tоб - постоянная времени объекта;
tоб - время запаздывания.
Эти параметры определяются, как правило, графически следующим образом:
- возможно точнее строится кривая разгона в удобном масштабе. Кривая не должна иметь изломов и выбросов, при необходимости следует выполнить графическое сглаживание данных;
- в точке максимальной скорости изменения выходной переменной (в точке перегиба) проводят касательную к кривой разгона до пересечения ее, с одной стороны, с осью абсцисс, с другой – с линией установившегося значения выходной переменной. Отрезок времени между этими точками есть Tоб ;
- tоб есть отрезок времени от 0 до пересечения касательной с осью абсцисс;
- kоб определяют по формуле
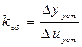 |
 |
Процедура определения параметров объекта регулирования поясняется на рис. 3.2.
Рисунок 3.2 – Определение параметров объекта регулирования в виде апериодического звена с запаздыванием
Этот вид передаточной функции отличается простотой и легкостью определения параметров. Его недостатком является неточность полученного результата, тем не менее, он широко используется для приближенного расчета типовых регуляторов.
 2) Объект представлен дифференциальным уравнением 2-го порядка с транспортным запаздыванием.
2) Объект представлен дифференциальным уравнением 2-го порядка с транспортным запаздыванием.
где t - транспортное запаздывание,
a1, a2 - коэффициенты,
kоб - коэффициент передачи объекта.
Параметры этой передаточной функции могут быть определены разными методами, мы рассмотрим метод площадей Симою. Он выполняется в следующей последовательности:
 |
- строят кривую разгона и по ней определяют t как время от 0 до начала изменения выходной переменной. Выполняют разбиение отрезка времени от начала изменения кривой разгона до установившегося значения на равные интервалы Dt . Значение Dt выбирают так, чтобы на участках разбиения y(t) мало отличалось от прямой. На рис. 3.3 представлено подобное разбиение;
Рисунок 3.3 – Разбиение кривой разгона на участки
- определяют коэффициенты передаточной функции по формулам
 |
где - кривая разгона в безразмерной форме без транспортного запаздывания,
t' = t - tоб .
n – количество интервалов разбиения кривой разгона, n = 19;
ΔYб(i) – значение безразмерной кривой разгона в i-й момент времени (см. таблицу 6 ниже);
Δt – интервал разбиения, численно равный Mt .
Коэффициент передачи объекта kоб определяется так же, как в методе касательной.
Например, kоб=1,35 °С/%, a1=15,1 сек, a2=35,2 сек2. Тогда искомая передаточная функция имеет вид

По расчету настроечных параметров регуляторов
Существует много способов определения настроечных параметров типовых регуляторов. Они отличаются используемыми критериями качества регулирования и точностью. В данной работе используется приближенный способ определения настроечных параметров. Для него применяется уже известная нам аппроксимация объекта управления инерционным звеном с запаздыванием, которая выражается передаточной функцией
 |
В таблицу 5 помещены приближенные формулы для определения приближенных значений настроечных параметров различных регуляторов. Исходными данными для этих формул являются параметры приведенной передаточной функции объекта.
Таблица 5
Формулы для определения настроечных параметров регуляторов
| регулятор |  Апериодический переходный процесс Апериодический переходный процесс
| |
| П | 
| |
| И | 
| |
| ПИ | 
|
2 Методические указания к выполнению расчетной работы № 4
Кривая разгона для любого варианта задана двумя масштабами (Mt и MY) и величиной ступенчатого изменения управляющего воздействия DUст. Эти данные есть у студентов в их заданиях.
Фактическая кривая разгона получается пересчетом безразмерной кривой разгона, общей для всех вариантов, по формулам
t = Mt tБ, ,
DY = MY DYБ ,
где t – реальное время;
tБ – безразмерное время;
Mt – масштаб времени;
DY – изменение регулируемой переменной в натуральных единицах;
DYБ – изменение регулируемой переменной в безразмерном виде;
MY – масштаб для регулируемой переменной.
Масштабы Mt,MY, а также величина ступенчатого изменения управляющего воздействия (управления) при снятии кривой разгона DUст свои для каждого задания и являются частью этих заданий.
Значения безразмерных ординат кривой разгона в дискретные моменты безразмерного времени приведены в таблице 1
Таблица 6 - Безразмерная кривая разгона, общая для всех вариантов
| tб | |||||||
| DYб | 0.01 | 0.07 | 0.25 | 0.43 | 0.58 | 0.7 | |
| tб | |||||||
| DYб | 0.78 | 0.84 | 0.88 | 0.91 | 0.94 | 0.96 | 0.97 |
| tб | |||||||
| DYб | 0.98 | 0.985 | 0.99 |
3 Содержание отчета
В отчете по работе должно быть:
1) исходные данные по своему варианту и безразмерная кривая разгона;
2) пересчитанная кривая разгона;
3) рисунок, где построен график кривой разгона и выполнена аппроксимация по методу касательной;
4) передаточная функция по методу касательной;
5) формулы для расчета а1, а2 по методу Симою и вычисление коэффициентов а1, а2.
5) передаточная функция по Симою;
6) эмпирические формулы для расчета настоечных параметров П и ПИ регуляторов и вычисление этих параметров. Алгоритмы П и ПИ регулирования в общем виде и с числовыми коэффициентами.
4 Контрольные вопросы при защите работы
1) Что такое аппроксимация кривой разгона?
2) Назовите этапы экспериментального метода аппроксимации кривой разгона.
3) Каковы условия снятия кривой разгона?
4) В чем заключается метод касательной при аппроксимации кривой разгона?
5) Выполните аппроксимацию нарисованной преподавателем кривой разгона методом касательной.
6) Запишите передаточную функцию, получающуюся по методу касательной.
7) Запишите передаточную функцию, получающуюся по методу площадей Симою.
8) Каковы преимущества и недостатки метода Симою?
9) Запишите формулы для расчета настоечных параметров ПИ регулятора.
| <== предыдущая страница | | | следующая страница ==> |
| | | МЕТОДИЧЕСКИЕ УКАЗАНИЯ к дипломному проектированию по специальности «Экономика и управление на предприятии (в машиностроении)» |
Дата добавления: 2014-11-24; просмотров: 923; Нарушение авторских прав

Мы поможем в написании ваших работ!