Центральная предельная теорема. Снова рассмотрим последовательность случайных величин {xi} и найдём закон распределения zn= x1+

Снова рассмотрим последовательность случайных величин {x_i} и найдём закон распределения z_n= x₁+ ... + x_nсуммы этих случайных величин при неограниченном возрастании n. Оказывается, что закон распределения такой суммы при весьма общих условиях близок к нормальному закону. Этот факт определяет особое значение нормального распределения в теории вероятностей и имеет огромное прикладное значение. Соответствующее утверждение называется центральной предельной теоремой. Её строгое доказательство при достаточно общих предположениях впервые было дано русским математиком А.М. Ляпуновым. В частности, она верна для случая, когда xiодинаково распределены и имеют математическое ожидание a и дисперсию s2.

Теорема Ляпунова(точнее, её частный случай для одинаково распределенных слагаемых). Пусть {xi} - последовательность независимых случайных величин и

.

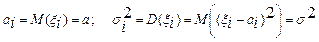Если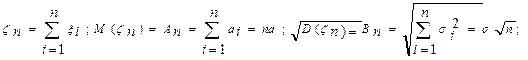

то 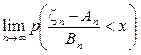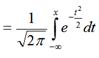. (2.24)

Отсюда следует, что случайная величина 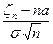распределена асимптотически нормально с параметрами 0 и 1 , а znраспределена приблизительно нормально с параметрами na и .

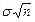Единственное условие теоремы Ляпунова состоит в существовании дисперсии слагаемых (одинаково распределённых). В общем случае эта теорема много шире (не требует одинаковости распределений слагаемых).

Интегральная теорема Муавра-Лапласа. Рассмотрим последовательность независимых, однородных испытаний (схема Бернулли), в каждом из которых событие A может появиться с вероятностью p. Вероятность того, что событие A появится при этом не менее m₁и не более m₂раз, определяется по формуле Бернулли

,

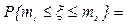
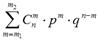причём, при большом n применение этой формулы практически невозможно и применяется интегральная теорема Муавра-Лапласа. Для её обоснования рассмотрим последовательность случайных величин {xi}, принимающих значение 1, если событие произошло, и 0, если не произошло (индикаторов испытаний). Сумма индикаторов, то есть 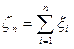, равна числу появлений события A при n испытаниях (то есть m), причём

.

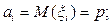
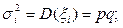
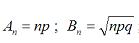Условия теоремы Ляпунова выполнены, поэтому случайная величина zn= m распределена асимптотически нормально с математическим ожиданием a = np и среднеквадратическим отклонением 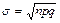. Остаётся найти вероятность того, что случайная величина zn= m будет заключена в пределах от m₁до m₂.

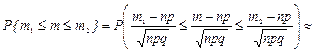
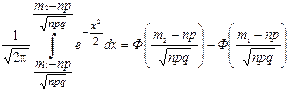, (2.25)

где Ф(x) - функция Лапласа. Тем самым обоснована интегральная теорема Муавра-Лапласа.

Итак, по теореме Муавра-Лапласа величина 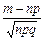распределена приблизительно нормально.Из таблиц нормального распределения видно, что:

.

.

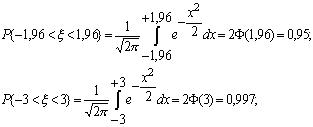
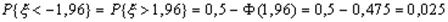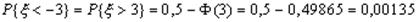Написанные соотношения означают, что с вероятностью 0,95 нормальная стандартная величина по модулю не превосходит числа 1,96, а с вероятностью 0,997 – числа 3. Аналогично выписываются односторонние пределы для x.

Таким образом, с вероятностью 0,95 выполняется

;

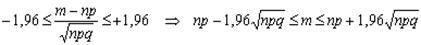а с вероятностью 0,997 выполняется

;

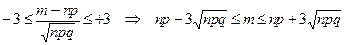а вероятность нижеприведенных неравенств 0,025

;

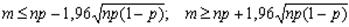а вероятность таких неравенств, когда в них 1,96 заменено на 3, вообще 0,001.

Можно для Х~N(a,s) определить число kbкак корень уравнения 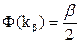(он находится по таблице – для b= 0,95 kb= 1,96, для b= 0,997 kb= 3) и сказать, что с вероятностьюbвыполняется

|X-a|<k_b^s. (2.26)

Тогда с вероятностью b выполняется

.

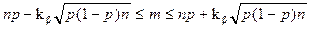Если мы введем ошибку a=1-b, то вероятность не попасть в односторонний интервал, определяемый k_b, будет a/2, то есть

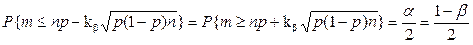. (2.27)

Эти формулы являются прямым следствием из теоремы Муавра-Лапласа.

Пример. 900 раз бросали монету, и герб выпал 490 раз. Что мы можем сказать о симметричности монеты?

Решение. Если монета симметрична, то p=1/2, q=1/2, np = 450 и

;

.

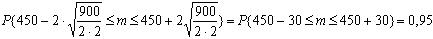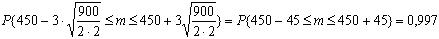Следовательно, мы можем сказать, что “на 95% мы уверены, что монета несимметрична”, но сказать, что мы уверены в этом на 99,7%, мы уже не можем.

Дата добавления: 2014-03-11; просмотров: 708; Нарушение авторских прав

Мы поможем в написании ваших работ!