Детерминированные модели

Классификация моделей потока

ТЕМА 4. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ТРАНСПОРТНОГО ПОТОКА

При исследованиях и проектировании ОДД приходится прибегать к описанию транспортных потоков математическими методами. Первостепенными задачами, послужившими развитию моделирования транспортных потоков, явились изучение и обоснование пропускной способности

магистралей и их пересечений. Поведение транспортного потока очень изменчиво и зависит от действия многих факторов.

Известные и нашедшие практическое применение в ОДД математические модели можно разделить на две группы в зависимости от подхода: детерминированные и вероятностные (стохастические).

К детерминированным относятся модели, в основе которых лежит функциональная зависимость между отдельными показателями, например, скоростью и дистанцией между автомобилями в потоке. При этом принимается, что все автомобили удалены друг от друга на одинаковое расстояние.

Стохастические модели отличаются большей объективностью. В них транспортный поток рассматривается как вероятностный (случайный) процесс. Например, распределение временных интервалов между автомобилями в потоке может приниматься не строго определенным, а случайным.

Простейшей математической моделью, описывающей поток автомобилей, является так называемая упрощенная динамическая модель. Ее применяют для определения максимально возможной интенсивности движения по одной полосе дороги N_{a max} при скорости n_а:

N_{a max} = Аn_а/L_Д, (4.1)

где А – коэффициент размерности.

При выражении скорости в километрах в час, а динамического габарита в метрах формула (4.1) является выражением для определения пропускной способности полосы

Р_п = 1000n_а/L_Д, (4.2)

Данная математическая модель составлена на основании двух упрощающих допущений: скорость всех транспортных единиц в потоке одинакова; транспортные средства однотипны, т.е. имеют равные динамические

габариты. Динамический габарит L_Д транспортного средства l_а, дистанции безопасности d и зазора l_о до остановившегося впереди автомобиля. Зазор l_о для легковых автомобилей колеблется в пределах 1-3 м.

Рассмотрим три подхода к определению динамического габарита L_Д.

1. При расчете минимальной теоретической дистанции исходят из абсолютно равных тормозных свойств пары автомобилей и учитывают только время реакции ведомого водителя t_p. Тогда L_Д = l_а +n_а t_p + l_о, а уравнение (4.1) приобретает линейный характер. В этом случае возможная интенсивность транспортного потока не имеет предела по мере увеличения скорости. Однако это не соответствует реальным характеристикам водителей и приводит к завышению возможной интенсивности потока. Здесь главную роль играет практическое значительное увеличение t_p при высоких скоростях.

2. При расчете на "полную безопасность" исходят из того, что дистанция d должна быть равна полному остановочному пути заднего (второго) автомобиля S_о2. Тогда динамический габарит

L_Д = l_а +n_а t_p + n²_а/2j_а + l_о.

В этой упрощенной формуле не выделен отрезок, проходимый за время нарастания замедления, а учитывается только установившееся замедление j_а. В этом случае уравнение (4.1) приобретает вид квадратичной функции, а интенсивность имеет предел при определенном значении скорости n_а (скорости транспортного потока). Такой подход больше соответствует требованиям обеспечения безопасности движения при высоких скоростях (более 90 км/ч).

3. Наиболее реальный подход основан на той предпосылке, что при расчете дистанции безопасности d надо учитывать разницу тормозных путей (или замедлений) автомобилей, а также то обстоятельство, что "лидер" в процессе торможения также перемещается на расстояние, равное своему тормозному пути.

Американскими специалистами была предложена теория "следования за лидером", математическим выражением которой является микроскопическая модель транспортного потока. Микроскопической ее называют потому, что она рассматривает элемент потока – пару следующих друг за другом транспортных средств. Особенностью этой модели является то, что в ней отражены закономерности комплекса ВАДС и, в частности, психологический аспект управления автомобилями. Он заключается в том, что при движении в плотном транспортном потоке действия водителя обусловлены изменениями скорости лидирующего (ведущего) автомобиля и дистанции до него.

Экспериментальная проверка основного уравнения осуществлялась методом натурального имитационного эксперимента с помощью двух автомобилей, оборудованных аппаратурой для измерения значений параметров уравнения. Дистанцию между автомобилями определяли киносъемкой. Однако такой эксперимент содержит искусственность, искажающую реальный процесс. Это заключается в специальном подборе водителей, автомобилей и задании режима движения. Кроме того, относительно малое число замеров не позволяет охватить все многообразие ситуаций, возникающих в реальном потоке. Дорожные условия рассматриваются в данной модели не в качестве отдельных параметров, а как проявляющиеся в значении скорости движения. Уравнение теории следования за лидером описывает взаимодействие между автомобилями с учетом реакции водителя на изменения в транспортном потоке, называемые стимулами.

К моделям, рассматривающим поток в целом и называемым макроскопическими, относят модели гидродинамической теории. Одна из них основана на уравнении неразрывности, которое обуславливает постоянство количества жидкости при ее протекании по водостоку, и в обозначениях, принятых для транспортного потока, имеет вид:

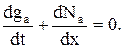
В результате преобразований и упрощений интенсивность транспортного потока

N_a = n_а g_a ln(g_{a max} /g_а),

где n_а – скорость, подлежащая экспериментальному определению;

g_{a max} – плотность транспортного потока при заторе.

Вторая гидродинамическая модель использует известное из гидравлики понятие о потенциале давления жидкости и предполагает, что движение автомобиля выражается в виде функции некоторого потенциала давления, зависящего от дорожных условий и психофизиологического состояния водителя.

Дата добавления: 2014-03-11; просмотров: 712; Нарушение авторских прав

Мы поможем в написании ваших работ!