Стохастические модели

Для решения некоторых задач ОДД необходимо располагать стохастическими характеристиками параметров транспортных потоков в зоне пересечений или на других контролируемых участках дорог. Исследованиями установлено, что для описания потоков сравнительно малой интенсивности, характеризующих вероятность проезда определенного числа транспортных средств через сечение дороги, применимо уравнение (распределение) Пуассона.

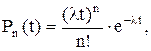(4.3)

где P_n(t) – вероятность проезда n-го числа автомобилей за время t;

l – основной параметр распределения (интенсивность транспортного потока), авт/с;

t – длительность отрезков наблюдения, с;

n – число наблюдаемых автомобилей .

Практически для целей управления движения более необходимо располагать данными о характере расширения временных интервалов между следующими друг за другом транспортными средствами.

Если появление автомобилей характеризуется распределением P_n(t), то интервалы между автомобилями распределены по экспоненциальному закону:

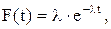
где F(t) – плотность распределения.

Следует отметить, что в транспортном потоке физически невозможно появление интервалов, меньших, чем соответствующие длине типичного транспортного средства (например, 4-5 м для потока легковых автомобилей).

Поэтому более правильным для описания распределения временных интервалов оказывается использование модели смешанного экспоненциального закона:

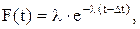
Dt – временной интервал, соответствующий характерной длине транспортного средства.

Упомянутые модели дают удовлетворительную сходимость с натурными наблюдениями, состоящими, главным образом, из легковых автомобилей. При смешанном потоке распределение Пуассона не дает удовлетворительных результатов. В этом случае может быть применено гамма-распределение Пирсона Ш типа или распределение Эрланга.

Движение транспортных средств по дорогам в потоке большей интенсивности и, особенно в зоне пересечений может быть рассмотрено на основе теории массового обслуживания.

Применительно к транспортной задаче это означает возможность определения пропускной способности пересечения и задержек автомобилей.

Взаимосвязь интенсивности, скорости и плотности потока на одной полосе дороги графически может быть изображена в виде основной диаграммы транспортного потока.

N_a = V_a × g_a, авт/ч.

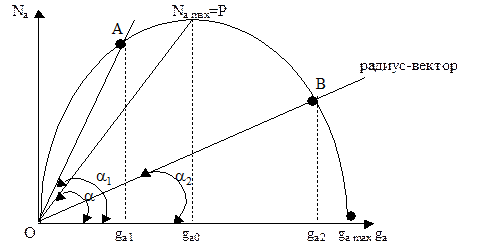
В точках 0 и g_{а max} интенсивность движения N_а = 0, т.е. либо произошел затор, либо на дороге нет транспортных средств.

Радиус-вектор, проведенный из точки 0 в направлении любой точки на кривой (А или В), характеризующий N_а, определяет значение средней скорости потока:

.

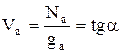Значение графика заключается в том, что по нему прослеживается зависимость, характеризующая безопасный транспортный поток – по мере роста плотности потока падает скорость. Высокие скорости могут быть получены в условиях относительно свободного движения транспортных средств.

На графике показаны две характерные точки:

А – для устойчивого движения транспортного потока;

В – для неустойчивого, близкого к заторовому состоянию потока.

Угол наклона радиуса-вектора в первой точке a₁ @ 60 ⁰ (tga =1,77), а во второй a₂ @ 15 ⁰ (tga =0,26).

Скорость в точке В (~9,9 км/ч), а в точке А (~67 км/ч), т.е. разница в 6,8 раз.

Следует, однако, отметить, что это не может отразить всю сложность процессов, происходящих в транспортном потоке, и характеризует его

лишь при однородном составе и нормальном состоянии дороги и внешней среды.

При изменении профиля дороги, состояния покрытия, условий видимости, состава потока – изменяется и характер диаграммы.

Дата добавления: 2014-03-11; просмотров: 507; Нарушение авторских прав

Мы поможем в написании ваших работ!