
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Решение. Устраним индуктивную связь и получим эквивалентную Т-схему четырёхполюсника (рис
Устраним индуктивную связь и получим эквивалентную Т-схему четырёхполюсника (рис. 5.10,б), у которого
Z1 = -jхС + j(х1+хМ) = -j35 + j(20 + 10) = -j5 Ом,
Z2 = -jхМ = -j10 Ом,
Z0 = j(х2+хМ) = j(60 + 10) = j70 Ом.
Для Т-схемы четырёхполюсника связь между коэффициентами и сопротивлениями установлена:
A = 1 + 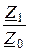 = 1 + (-j5)/(j70) = 0,928;
= 1 + (-j5)/(j70) = 0,928;
B = Z1+ Z2+ 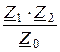 = -j5 – j10 +
= -j5 – j10 + 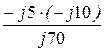 = -j15,70 Ом;
= -j15,70 Ом;
C = 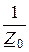 =
= 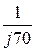 = -j0,0143 См;
= -j0,0143 См;
D = 1 + 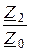 = 1 +
= 1 + 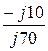 = 0,857.
= 0,857.
Ток нагрузки I2= 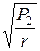 =
= 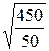 = 3 А.
= 3 А.
Примем I2= 3 А, по закону Ома U2= I2×Z2= 3×50 = 150 B.
Далее U1= А×U2 + B×I2 = 0,928×150 + (-j15,7)×3 = 147×e –j18,7° B,
I1= С×U2 + D×I2 = -j0,0143×150 + 0,857×3 = 3,35×e –j39,8° А,
P1= Re(U1× 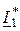 ) = Re(147×e –j18,7°×3,35×e j39,8°) = 459 Bт » P2= 450 Bт.
) = Re(147×e –j18,7°×3,35×e j39,8°) = 459 Bт » P2= 450 Bт.
Обратим внимание, что рассматриваемая схема четырёхполюсника яв-ляется схемой без потерь (без активных сопротивлений), для которой P1= P2. Расхождение в 9 Bт появилось вследствие округления результатов вычислений до трёх значащих цифр. При этом относительная погрешность вычислений по мощности составила e % = 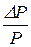 ×100 =
×100 = 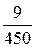 ×100 = 2%, что допустимо при выполнении расчётов с указанной точностью.
×100 = 2%, что допустимо при выполнении расчётов с указанной точностью.

ЗАДАЧА 5.9. Определить А-коэффициенты Х-схемы (мостовая схема) четырёхполюсника, пред-ставленного на рис. 5.11, если r = xL = xС = 10 Ом.
Указание. При отборе единственного значения коэффициента А рекомендуется построить диаграмму комплексных потенциалов четырёхполюсника для режима холостого хода, приняв j 1¢ = 0.
Ответы: А = 0,6 + j0,8, В = j20 Ом, С = 0,1 + j0,1 См, D = 1 + j2.
Задача 5.10. а) На зажимы источника переменного напряжения с ЭДС Е = 100 В и внутренним сопротивлением Zв = rв = 1 Ом подключена нагруз-ка Zн = rн = 9 Ом (рис. 5.12,а). Определить активную мощность приёмника Рн.
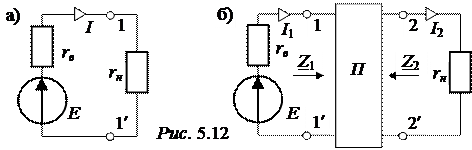 |
б) Для увеличения передаваемой в нагрузку активной мощности от генератора между генератором и нагрузкой включен четырёхполюсник (рис. 5.12,б). Определить параметры этого четырёхполюсника из условия передачи от генератора в нагрузку максимально возможной мощности Р2max.
Решениезадания а). Ток в цепи рис. 5.12,а
I = 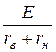 =
= 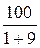 = 10 А,
= 10 А,
активная мощность приёмника Рн = I 2×rн = 10 2×9 = 900 Вт.
Решениезадания б). Нагрузкой генератора в схеме рис. 5.12,б является четырёхполюсник, на выходные зажимы которого подключен приёмник, сопротивление которого Zн = rн = 9 Ом. Задачу передачи максимальной мощности от генератора через четырёхполюсник к приёмнику будем решать в два этапа:
1. Подберём такое сопротивление нагрузки на генератор Z1, при котором на вход четырёхполюсника поступит максимально возможная мощность Р1max.
На основании основных уравнений четырёхполюсника при нагрузке Z2 = rн его входное сопротивление
Z1 = 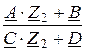 .
.
Так как четырёхполюсник ещё требуется подобрать, то его коэффициенты можно принимать любыми, изменяя таким образом нагрузку на генератор.
Заметим, что устройство, с помощью которого можно изменить (трансформировать) сопротивление нагрузки, называется трансформатором сопротивления, а задача подбора схемы с заданными свойствами (в рассматриваемом примере четырёхполюсника) называется задачей синтеза электрической цепи.
В разделах курса «Линейные цепи постоянного тока», «Линейные цепи синусоидального тока» изучен вопрос об условиях передачи максимальной активной мощности от активного двухполюсника к пассивному. При полной компенсации реактивной мощности в цепи генератора, что имеет место в условиях рассматриваемой задачи 5.10,а, это условие выражается равенством rв = rн.
Таким образом, первое расчётное уравнение для синтеза четырёхполюсника принимает вид: Z1 = 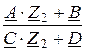 = rв. (1)
= rв. (1)
2. Рассматривая левую часть схемы рис. 5.12,б по отношению к выход-ным зажимам 2-2¢ четырёхполюсника как эквивалентный генератор с внут-ренним сопротивлением Z2 пассивной части схемы, запишем условие пере-дачи максимальной мощности от эквивалентного генератора в нагрузку rн:
Z2 = 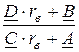 = rн. (2)
= rн. (2)
Для определения четырёх коэффициентов А, В, С, D требуется система четырёх линейно независимых уравнений. Третье расчётное уравнение определяется свойством коэффициентов четырёхполюсника
АD – ВС = 1. (3)
Недостающее четвёртое уравнение позволяет нам свободу выбора вплоть до принятия одного коэффициента любым комплексным числом. Таким образом, задача синтеза четырёхполюсника, необходимого для увеличения передаваемой мощности в приёмник, имеет бесконечно большое число решений.
Обычно для получения четвёртого расчётного уравнения поступают одним из двух способов:
1. Синтезируют симметричный четырёхполюсник, когда А = D и для реализации принимают простейшие из схем: Т-образный или П-образный четырёхполюсник;
2. Принимают коэффициент D = 1, и тогда и Т-, и П-схема превраща-ется в несимметричную Г-схему вида рис. 5.14,а.
Приведём решение обоих вариантов.
1. Синтез симметричного четырёхполюсника.
Коэффициенты искомого четырёхполюсника определяются системой уравнений:
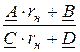 = rв;
= rв; 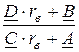 = rн; АD – ВС = 1; А = D.
= rн; АD – ВС = 1; А = D.
Приведём подробное решение системы:
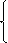 А×rн + В = С×rв×rн + D×rв, учтём А = D, а затем вычтем второе
А×rн + В = С×rв×rн + D×rв, учтём А = D, а затем вычтем второе
D×rв + В = С×rв×rн + А×rн. уравнение из первого. Получим:
А×(rн – rв) = А×(rв – rн), откуда А = 0 = D.
Для определения двух оставшихся коэффициентов решаем систему уравнений, в которой учтено А = D = 0:
В = С×rв×rн; -ВС = 1, откуда В = ±j 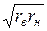 , С = ±j
, С = ±j 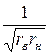 ,
,
причём с учётом -ВС = 1 знаки при мнимой единице j должны быть одина-ковыми для В и С.
Получаем два варианта решения:
а) А = D = 0; б) А = D = 0;
В = +j 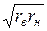 = j
= j 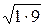 = j3 Ом; В = -j
= j3 Ом; В = -j 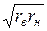 = -j
= -j 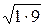 = -j3 Ом;
= -j3 Ом;
С = +j 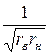 = j
= j 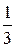 См. С = -j
См. С = -j 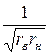 = -j
= -j 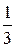 См.
См.
Рассчитываем параметры типовых Т- и П-схем четырёхполюсников по известным коэффициентам:
- для Т-схемы Z1Т = Z2Т = 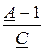 = ± j3 Ом, Z0Т =
= ± j3 Ом, Z0Т = 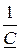 =
= 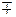 j3 Ом.
j3 Ом.
- для П-схемы Z1П = Z2П = 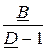 =
= 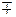 j3 Ом, Z0П = В = ± j3 Ом.
j3 Ом, Z0П = В = ± j3 Ом.
В ответах верхние знаки относятся к варианту а), нижние – к варианту б). Соответствующие схемы с указанием сопротивлений в Ом приведены на рис. 5.13.

При использовании любой из этих схем Z1 = rв = 1 Ом,
ток в цепи генератора станет I1 = 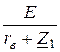 =
= 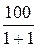 = 50 А,
= 50 А,
активная мощность на входе четырёхполюсника
Р1max = I 2×Z1= 50 2×1 = 2500 Вт.
Так как четырёхполюсник выполнен из реактивных элементов, не имеет потерь, то активная мощность приёмника Р2max = Р1max = 2500 Вт
вместо Р2= 900 Вт исходной схемы рис. 5.12,а.
2. Синтез Г-схемы четырёхполюсника.
Коэффициенты искомой схемы четырёхполюсника определим решением системы уравнений
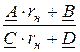 = rв;
= rв; 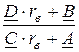 = rн; АD – ВС = 1; D = 1.
= rн; АD – ВС = 1; D = 1.
Из этой системы получаем два варианта решения:
а) А = 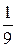 ; В = j2
; В = j2 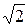 Ом; С = j
Ом; С = j 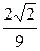 См; D = 1;
См; D = 1;
 |
б) А =
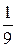 ; В = -j2
; В = -j2 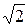 Ом; С = -j
Ом; С = -j 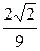 См; D = 1;
См; D = 1;
Этим вариантам соответствуют только две Г-схемы, приведенные на рис. 5.14.
На рис. 5.14 сопротивления индуктивных и ёмкостных элементов представлены в Ом. Здесь так же, как и в случае применения схем рис. 5.13
Р1max = Р2max = 2500 Вт, I1= 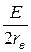 =
= 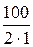 = 50 А.
= 50 А.
Ток нагрузки можно определить по формуле I2= 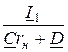 .
.
Например, для схемы рис. 5.14,а он равен
 I2=
I2= 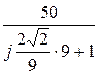 =
= 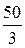 ×e –j70,53° А.
×e –j70,53° А.
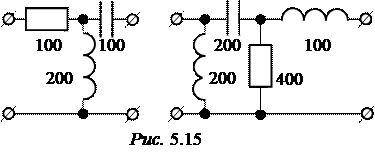
ЗАДАЧА 5.11. Эквива-лентность четырёхполюсни-ков. Сопротивления элемен-тов на схемах (рис. 5.15) даны в Омах.
Необходимо показать, что приведенные четырёхполюсники эквивалентны.
Указания. Поскольку четырёхполюсники обратимы, достаточно сравнить значения сопротивлений Z1Х, Z1К у обоих 4-полюсников.
В нашем примере: Z1Х = 100 + j200 Ом, Z1К = 100 – j200 Ом,
Z2Х = +j100 Ом, Z2К = 80 – j 60 Ом.
Значения сопротивлений со вторичных зажимов приведены просто для контроля.
 Задача 5.12. Симметричный 4х-полюсник с rнг = 5 кОм питается от источника Е1 = 48 В (рис. 5.12б). При замкнутом рубильнике S ток на входе I1 = 3,2 мA, на выходе I2 = 1,6 мА.
Задача 5.12. Симметричный 4х-полюсник с rнг = 5 кОм питается от источника Е1 = 48 В (рис. 5.12б). При замкнутом рубильнике S ток на входе I1 = 3,2 мA, на выходе I2 = 1,6 мА.
Определить А-коэффициенты четырёхполюсника и найти токи при разомкнутом рубильнике.
Методические указания: необходимо записать уравнения для режима короткого замыкания. Это позволит найти А-коэффициенты 4-полюсника.
Ответы: I1 = 3 мA, I2 = 1,2 мА.
 Задача 5.13. На выходе симметричного 4х-полюсника, нагруженного на сопротивление Zнг = Zc и имеющего коэффи-циенты A = 1+ j1, B = 10 + j10 Ом, протекает ток I2 = 2 A. Рассчитайте ток и напряжение на входе четырёхполюсника.
Задача 5.13. На выходе симметричного 4х-полюсника, нагруженного на сопротивление Zнг = Zc и имеющего коэффи-циенты A = 1+ j1, B = 10 + j10 Ом, протекает ток I2 = 2 A. Рассчитайте ток и напряжение на входе четырёхполюсника.
Ответы: U1 = 54,65×е j38,52° В,
I1 = 5,777×е j51,8° А, Zc = 9,46×е –j13,28° Ом.
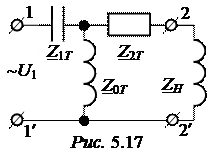
Задача 5.14. Четырёхполюсник с известными А-параметрами (А = = 0,5; В =10 + j10 Ом; С = -j0,05 См; D =1 – j1) собран по Т-схеме (рис. 5.17) и нагружен сопротивлением ZH = 20×е +j90° Ом. Требуется рассчитать токи на входе и выходе четырёхполюсника, построить векторную диаграмму.
Методические указания: начать следует с определения сопротивлений четырёхполюсника. Они будут нужны для построения векторной диаграммы.
Ответы: I1 = 20 – j10 А; I2 = 10 A.
Задача 5.15. Для симметричного четырёхполюсника экспериментально установлено, что Z1Х = 10×е +j90° Ом, Z2К = 10×е +j30° Ом. Требуется определить А-параметры четырёхполюсника и угол сдвига фаз между входными напряжением и током при согласованной нагрузке.
Ответы: А = D = 1·е -j30°; В = 10 Ом; С = 0,1×е –j120° См; j = jC = 60°.
| <== предыдущая страница | | | следующая страница ==> |
| Решение. Расчёт коэффициентов выполним с помощью входных сопротивлений | | | Уравнения пассивных четырёхполюсников с характеристи-ческими параметрами |
Дата добавления: 2014-10-10; просмотров: 447; Нарушение авторских прав

Мы поможем в написании ваших работ!