
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Уравнения пассивных четырёхполюсников с характеристи-ческими параметрами
ЗАДАЧА 5.16. Для схемы задачи 5.1 рассчитать характеристические параметры Z1С, Z2С, Г, а, b. При напряжении на зажимах согласованной нагрузки U2 = 100 В определить U1, I1, используя основные уравнения четырёхполюсника с характеристическими параметрами.
Решение
При решении задачи 5.1 были определены коэффициенты четырёхполюсника:
А = 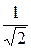 ×е –j45°, В = 10
×е –j45°, В = 10 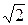 ×е –j45° Ом, С = 0,05×е –j90° См, D = 1.
×е –j45° Ом, С = 0,05×е –j90° См, D = 1.
Воспользуемся полученными значениями для расчёта характеристи-ческих параметров.
Характеристическое сопротивление со стороны входных зажимов
Z1С = 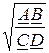 =
= 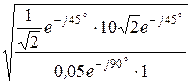 = 10
= 10 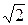 ×е j0° = 10
×е j0° = 10 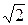 Ом,
Ом,
со стороны выходных зажимов
Z2С = 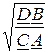 =
= 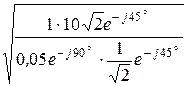 = 20×е j45° Ом.
= 20×е j45° Ом.
Заметим, что извлечение корня из комплексного числа приводит к бесконечно большому количеству ответов.
Характеристические сопротивления имеют другое название: волновые сопротивления той среды, в которой распространяются электромагнитные волны: ZС = ZВ = 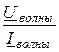 = ZС ·е jjс, где Uволны, Iволны – комплексы напряжения и тока движущейся волны.
= ZС ·е jjс, где Uволны, Iволны – комплексы напряжения и тока движущейся волны.
Как известно из курса ТОЭ, для любой среды при положительном моду-
ле ZС (полное сопротивление) аргумент jС комплексного числа не может превышать 90°. По этому принципу осуществлён отбор приведенных ранее числовых значений для Z1С и Z2С.
Постоянная передачи проходного четырёхполюсника
Г = ln 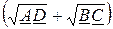 = ln
= ln 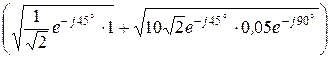 =
=
= ln 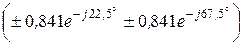 .
.
В результате под знаком натурального логарифма могут находиться 4 числа:
1) 1,099 – j1,099 = 1,554×е -j45°, 2) 0,455 + j0,455 = 0,64×е j45°,
3) -0,455 – j0,455 = 0,64×е –j135°, 4) -1,099 + j1,099 = 1,554×е j135°.
Комплексное число в показательной форме записи имеет выражение
M = m×е jm.
Так как Г = lnM и Г = a + jb, то a = ln(m) нп и b = m рад. кроме того, коэффициент затухания a > 0 для схемы с потерями, исходя из физического смысла: при движении волны в среде с потерями её энергия уменьшается.
Для чисел п.2 и п.3 расчётов a = ln0,64 = -0,446 < 0, что противоречит физике процесса.
Остаётся единственный ответ a = ln1,554 = 0,441 нп, рассчитанный при логарифмировании чисел п.1 и п.4.
При этом получаем 2 значения коэффициента фазы:
b1= -45° 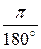 = -0,785 рад < 0, b2= 135°
= -0,785 рад < 0, b2= 135° 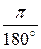 = 2,36 рад > 0.
= 2,36 рад > 0.
Отбор единственного значения b (положительного или отрицательного) выполним с помощью векторной диаграммы четырёхполюсника, согласованного с нагрузкой (рис. 5.18).
На векторной диаграмме показаны углы между напряжениями U2 и U1:
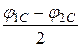 + b < 0,
+ b < 0,
между токами I2 и I1: 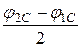 + b < 0.
+ b < 0.
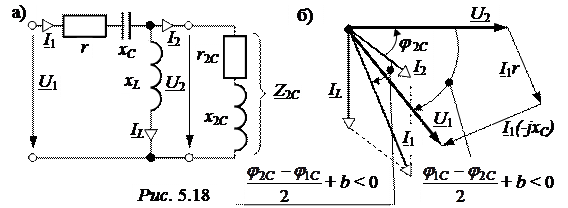 |
Эти углы соответствуют соотношениям, полученным из основных уравнений четырёхполюсника для согласованного режима:
U1 = 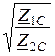 ·U2е Г , I1 =
·U2е Г , I1 = 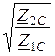 ·I2е Г , а
·I2е Г , а 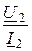 = Z2C.
= Z2C.
Подсчитаем 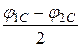 =
= 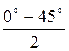 = -22,5°, тогда
= -22,5°, тогда 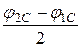 = +22,5°.
= +22,5°.
Так как угол между токами 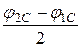 + b = (+22,5° + b) < 0, то b < 0.
+ b = (+22,5° + b) < 0, то b < 0.
Остаётся один ответ: b = b1= -0,785 рад, а постоянная передачи
Г = a + jb = 0,441 – j0,785.
Напряжение и ток на входе четырёхполюсника при согласованной нагрузке:
U1 = 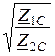 ·U2е Г =
·U2е Г = 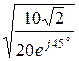 ·100е 0,441×е -j45° = 130,7×е –j67,5° В,
·100е 0,441×е -j45° = 130,7×е –j67,5° В,
I1 = 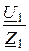 =
= 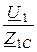 =
= 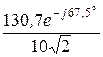 = 9,24×е –j67,5° А.
= 9,24×е –j67,5° А.
ЗАДАЧА 5.17. Определить характеристические параметры четырёхпо-люсника рис. 5.19,а, если r1 = r2 = 10 Ом, xL = 20 Ом, xC = 10 Ом.
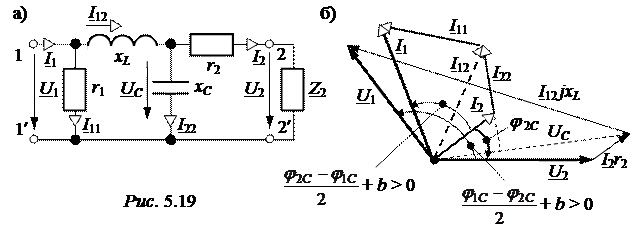
Решение
Расчёт выполним с помощью входных сопротивлений четырёхполюсника.
Z1X = 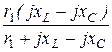 =
= 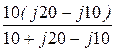 = 5 + j5 = 5
= 5 + j5 = 5 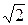 ×e j45° Ом,
×e j45° Ом,
Z1К = 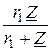 , где Z = jxL +
, где Z = jxL + 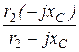 = j5 +
= j5 + 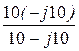 = 5 + j15 Ом,
= 5 + j15 Ом,
тогда Z1К = 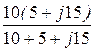 =
= 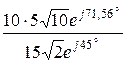 =
= 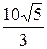 ×e j26,56° Ом.
×e j26,56° Ом.
Z2X = r2 + 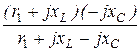 = 10 +
= 10 + 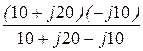 = 15 – j15 = 15
= 15 – j15 = 15 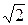 ×e -j45° Ом,
×e -j45° Ом,
Z2К = r2 + 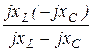 = 10 +
= 10 + 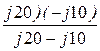 = 10 – j20 = 10
= 10 – j20 = 10 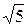 ×e –j63,44° Ом.
×e –j63,44° Ом.
Характеристические сопротивления
Z1С = 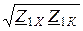 =
= 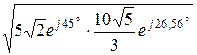 = 7,26×e j35,78° Ом,
= 7,26×e j35,78° Ом,
Z2С = 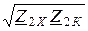 =
= 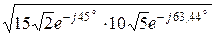 = 21,78×e -j54,22° Ом.
= 21,78×e -j54,22° Ом.
Далее thГ = 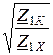 =
= 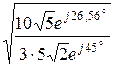 = 1,027×e –j9,22° = 1,013 – j0,165,
= 1,027×e –j9,22° = 1,013 – j0,165,
e 2Г= e 2а·e j2b = 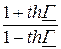 =
= 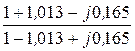 =
= 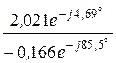 = -12,17×e j80,81°.
= -12,17×e j80,81°.
Этот ответ необходимо записать с положительным модулем, так как e 2а > 0, для чего к аргументу требуется добавить ±180°.
Получаем e 2а = 12,17, откуда коэффициент затухания четырёхполюс-ника а = ½·ln12,17 = 1,25 Нп.
Для определения коэффициента фазы получаем два соотношения
e j2·b1 = e j260,81°; e j2·b2 = e –j99,19°,
из которых получаем b1 > 0, b2 < 0.
Для определения знака коэффициента фазы построим векторную диаграмму четырёхполюсника при Z2 = Z2С (согласованный режим работы четырёхполюсника) (рис. 5.19,б). При этом основные уравнения четырёх-полюсника приобретают вид: U1 = 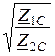 ·U2е Г , I1 =
·U2е Г , I1 = 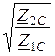 ·I2е Г .
·I2е Г .
Выполним вычисления:
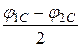 =
= 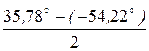 = +45°, а
= +45°, а 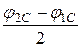 = -45°.
= -45°.
На векторной диаграмме (рис. 5.19,б) угол между векторами токов I2 и I1 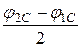 + b > 0, следовательно, b > 0, так как
+ b > 0, следовательно, b > 0, так как 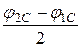 = -45° < 0.
= -45° < 0.
Таким образом, искомая величина b = ½·260,81° = 130,4° = 2,276 рад,
а постоянная передачи Г = а + jb = 1,25 + j2,276.
Замечание. При подсчёте постоянной передачи из формулы
e 2Г= e 2а·e j2b = 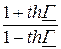 = m·e j(m +k·360°)
= m·e j(m +k·360°)
для аргумента комплексного числа получается бесконечное число ответов:
b = ½·m + k ·180°.
Если схема четырёхполюсника работает при фиксированной частоте, то практическое значение имеет только знак постоянной фазы при условии, что |b| < 180°.
При изменяющихся частотах требуется строить частотные характеристи-
ки электрических устройств, так как в зависимости от числа реактивных элементов схемы четырёхполюсника при изменении частоты w(0 … ¥) возможно изменение b(w) за пределы ±180°. (см. примеры исследования в разделе «Электрические фильтры»).
ЗАДАЧА 5.18. Для симметричного четырёхполюсника по опытам х.х. и к.з. найдено:
ZX = 27,63×e +j26,17° Ом, ZК = 45,1×e +j61° Ом.
Требуется определить характеристические параметры 4х-полюсника.
Ответ: Г = а + jb = 0,816 + j1,13, ZС = 35,3×e j43,59° Ом.
ЗАДАЧА 5.19. Четырёхполюсник задачи 5.17 (Z1С = 7,26×e j35,78° Ом, Z2С = 21,78×e -j54,22° Ом, Г = а + jb = 1,25 + j2,276) нагружен на сопротивление Z2= 40 + j30 Ом. Напряжение на входе U1 = 220 В. Используя основные уравнения с характеристическими параметрами, определить I1, P1, U2, I2, P2.
Решение
Исходные уравнения: U1 = 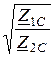 (U2×chГ + I2×Z2С ×shГ),
(U2×chГ + I2×Z2С ×shГ),
I1 = 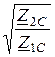 (
( 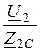 ×shГ + I2×chГ), U2 = I2×Z2.
×shГ + I2×chГ), U2 = I2×Z2.
Рассчитаем числовые значения гиперболических функций комплексного аргумента: Г = а + jb = 1,25 + j2,276 = 1,25 + j130,4°.
chГ = ch(а + jb) = ch(а)×cos(b) + jsh(а)×sin(b) =
= ch1,25×cos130,4°+ jsh1,25×sin130,4°= -1,225 + j1,22 = 1,73×e j135,1°,
shГ = sh(а + jb) = sh(а)×cos(b) + jch(а)×sin(b) =
= sh1,25×cos130,4°+ jch1,25×sin130,4°= -1,038 + j1,438 = 1,77×e j125,8°.
U2 = 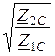
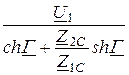 =
=
= 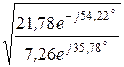
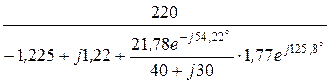 = 216,4×e -j154,6° B.
= 216,4×e -j154,6° B.
I2 = 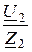 =
= 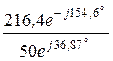 = 4,33×e -j191,5° A,
= 4,33×e -j191,5° A,
I1 = 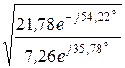 ×
× 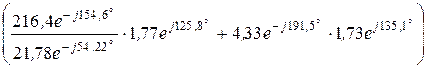 =
=
= 34,76×e –j41,26° A.
Активная мощность на входе четырёхполюсника
P1= Re(U1× 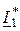 ) = Re(220×34,76×e j41,26°) = 5749 Bт;
) = Re(220×34,76×e j41,26°) = 5749 Bт;
активная мощность на выходе P2= I22×Re(Z2) = 4,332×40 = 750 Bт.
Фактическое ослабление сигнала по активной мощности
aфакт = ½×ln 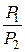 = ½×ln
= ½×ln 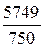 = 1,02 Нп.
= 1,02 Нп.
ЗАДАЧА 5.20. С помощью рассчитанных в задаче 5.17 характеристи-ческих параметров четырёхполюсника определить А-коэффициенты четырёх-полюсника рис. 5.19,а.
Решение
А = 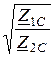 ×chГ =
×chГ = 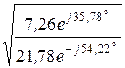 ×1,73×e j135°= 1×e j180°= -1.
×1,73×e j135°= 1×e j180°= -1.
Этот коэффициент легко проверяется по векторной диаграмме четырёхполюсника для режима холостого хода.
В = 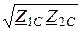 ×shГ =
×shГ = 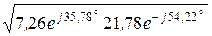 ×1,77×e j125,8°= 22,3×e j116,6° Ом,
×1,77×e j125,8°= 22,3×e j116,6° Ом,
C = 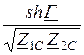 =
= 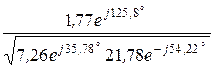 = 0,14×e j135° Cм,
= 0,14×e j135° Cм,
D = 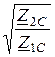 ×chГ =
×chГ = 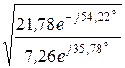 ×1,73×e j135°= 3×e j90°.
×1,73×e j135°= 3×e j90°.
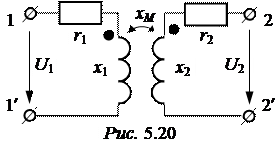
ЗАДАЧА 5.21. Для трансформато-ра рис. 5.20 определить коэффициенты A, В, C, D и характеристические парамет-ры, если: r1 = 6 Ом, r2 = 8 Ом,
x1 = 20 Ом, x2 = 12 Ом, xM = 8 Ом.
Ответы: А = 2,61×e –j16,7°;
В = 33,1×e j28,9° Ом; С = -j0,125 См; D = 1,8 ×e –j33,7°;
Z1С = 19,6×e j67,95° Ом, Z2С = 13,5×e j50,95° Ом, Г = А + jВ = 1,434 – j0,485.
Задача 5.22. Для определения характеристических параметров симметричного четырёхполюсника в опытах холостого хода и короткого замыкания получено:Z1X = j10 Ом, Z2К = 8,66 + j5 Ом.
Требуется определить характеристические параметры четырёхполюсника, записать уравнения через гиперболические функции.
Ответы: ZС = 10×e j60° Ом, Г = А + jВ = 0,658 – j0,785.
Задача 5.23. На выходе симметричного четырёхполюсника, нагруженного на сопротивление ZН = ZС и имеющего коэффициенты А = 1 + j1, В = 10 + j10 Ом, протекает ток I2 = 2 A. Рассчитать ток и напряжение на входе четырёхполюсника.
Ответы: ZC = 9,46×e –j13,28° Ом, U1 = 54,65×e j38,52° B, I1 = 5,777×e j51,8° A.
Задача 5.24. У симметричного четырёхполюсника известны характе-ристические параметры:
ZC = 9,461×e –j13,28° Ом, Г = 1,061 + j0,905 = 1,394×e +j40,45°.
Определить А-коэффициенты и составить Т-схему замещения.
Ответы: А = D = chГ = 1 + j1, В = 10 + j10 Ом, C = 0,05 + j0,15 Cм,
Z1T = Z2T = (А – 1)/C = 6 + j2 Ом, Z0T = C -1 = 2 – j6 Ом.
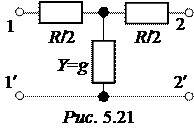 Задача 5.25. Для ослабления сигнала на а = = 17,4 дБ применён симметричный Т-образный ат-тенюатор (четырёхполюсник, работающий на постоянном токе) с характеристическим сопротивлением ZС = 100 Ом. Рассчитать параметры схемы аттенюатора (рис. 5.21) и определить мощность согласованной нагрузки, если мощность источника питания 200 мВт.
Задача 5.25. Для ослабления сигнала на а = = 17,4 дБ применён симметричный Т-образный ат-тенюатор (четырёхполюсник, работающий на постоянном токе) с характеристическим сопротивлением ZС = 100 Ом. Рассчитать параметры схемы аттенюатора (рис. 5.21) и определить мощность согласованной нагрузки, если мощность источника питания 200 мВт.
Методические указания: следует воспользоваться соотношениями, справедливыми для согласованного режима: Z1 = ZС, КПД h = e -2а; при работе четырёхполюсника на постоянном токе b = 0, Г = а.
Ответы: Р2 = 3,66 мВт, Z1T = Z2T = r/2 = 76,1 Ом, Z0T = g -1 = 27,8 Ом.
| <== предыдущая страница | | | следующая страница ==> |
| Решение. Устраним индуктивную связь и получим эквивалентную Т-схему четырёхполюсника (рис | | | Соединения четырёхполюсников |
Дата добавления: 2014-10-10; просмотров: 455; Нарушение авторских прав

Мы поможем в написании ваших работ!