
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Линейные дифференциальные уравнения с постоянными коэффициентами
Это уравнения, имеющие вид 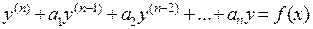 ,
,
где 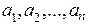 – постоянные коэффициенты.
– постоянные коэффициенты.
Однородным линейным уравнением  -го порядка называются уравнения вида
-го порядка называются уравнения вида 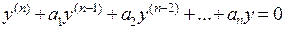 .
.
Решение однородного уравнения. Искать частное решение однородного уравнения будем в виде 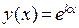 . Подставив
. Подставив 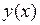 в указанном виде в однородное уравнение, получим
в указанном виде в однородное уравнение, получим 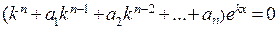 . Следовательно, неизвестное значение сомножителя
. Следовательно, неизвестное значение сомножителя 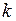 мы найдем, если решим алгебраическое уравнение
мы найдем, если решим алгебраическое уравнение  -й степени
-й степени
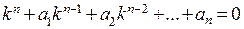 ,
,
называемое характеристическим уравнением.
В соответствии с основной теоремой алгебры характеристическое уравнение имеет ровно  корней, считая все вещественные и комплексные корни с учетом их кратности.
корней, считая все вещественные и комплексные корни с учетом их кратности.
Легко заметить, что если  – два линейно-независимых частных решения однородного уравнения, то
– два линейно-независимых частных решения однородного уравнения, то  также удовлетворяет тому же однородному уравнению при любых
также удовлетворяет тому же однородному уравнению при любых 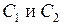 .
.
Рассмотрим все случаи корней характеристического уравнения и определим вид частного решения так, чтобы все частные решения были линейно-независимыми. Получив  линейно-независимых частных решений, мы сможем построить общее решение однородного уравнения
линейно-независимых частных решений, мы сможем построить общее решение однородного уравнения 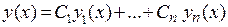 , содержащее
, содержащее  произвольных постоянных и позволяющее решать любую задачу Коши с начальными данными
произвольных постоянных и позволяющее решать любую задачу Коши с начальными данными 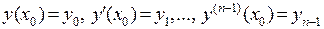 . Действительно, такая задача сведется к поиску конкретных значений постоянных
. Действительно, такая задача сведется к поиску конкретных значений постоянных 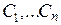 из системы линейных уравнений
из системы линейных уравнений
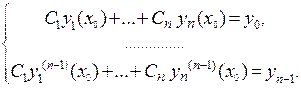
с ненулевым главным определителем системы
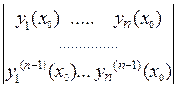 .
.
а) Простой вещественный корень. Простому вещественному корню 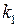 характеристического уравнения соответствует частное решение
характеристического уравнения соответствует частное решение 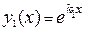 .
.
П р и м е р. Решить однородное дифференциальное уравнение 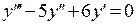 . Построим характеристическое уравнение
. Построим характеристическое уравнение 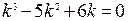 . Это характеристическое уравнение имеет три простых корня:
. Это характеристическое уравнение имеет три простых корня: 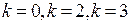 . Поэтому общим решение исходного дифференциального уравнение является функция
. Поэтому общим решение исходного дифференциального уравнение является функция 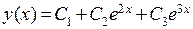 .
.
б) Вещественный корень кратности 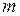 . Если корень
. Если корень 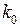 характеристического уравнения имеет кратность
характеристического уравнения имеет кратность 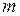 , то, естественно, мы не можем использовать
, то, естественно, мы не можем использовать 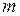 одинаковых частных решений вида
одинаковых частных решений вида 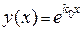 , соответствующих этому корню, так как эти решения будут линейно зависимыми. В указанном виде мы сможем взять только одно из
, соответствующих этому корню, так как эти решения будут линейно зависимыми. В указанном виде мы сможем взять только одно из 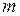 частных решений. Можно показать, что все
частных решений. Можно показать, что все 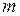 частных решений, соответствующих данному корню характеристического уравнения, имеют вид
частных решений, соответствующих данному корню характеристического уравнения, имеют вид 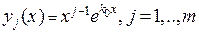 , то есть функции
, то есть функции 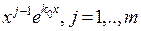 , удовлетворяют исходному однородному дифференциальному уравнению. Заметим прежде всего, что если
, удовлетворяют исходному однородному дифференциальному уравнению. Заметим прежде всего, что если 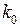 – корень уравнения
– корень уравнения 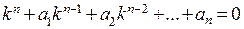 кратности
кратности 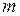 , то
, то 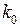 – корень любого из уравнений
– корень любого из уравнений 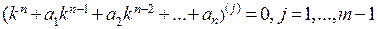 .
.
Покажем, как проводится доказательство того, что 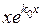 (случай
(случай 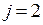 ) удовлетворяет исходному однородному уравнению. Подставим
) удовлетворяет исходному однородному уравнению. Подставим 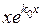 в левую часть исходного однородного дифференциального уравнения и получим
в левую часть исходного однородного дифференциального уравнения и получим
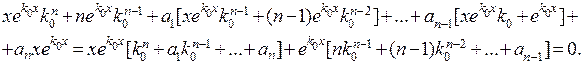
Первое выражение в квадратных скобках обращается в ноль, так как 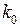 – корень характеристического уравнения, второе выражение в квадратных скобках обращается в ноль, так как
– корень характеристического уравнения, второе выражение в квадратных скобках обращается в ноль, так как 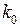 – корень уравнения
– корень уравнения 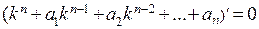 . Подобным же образом можно показать, что функции
. Подобным же образом можно показать, что функции 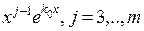 , удовлетворяют исходному однородному дифференциальному уравнению.
, удовлетворяют исходному однородному дифференциальному уравнению.
П р и м е р. Решить однородное дифференциальное уравнение 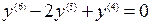 . Характеристическое уравнение имеет вид
. Характеристическое уравнение имеет вид 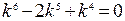 , и следовательно, имеет корни 0 (кратности четыре) и 1 (кратности два). Поэтому общим решением исходного дифференциального уравнения является функция
, и следовательно, имеет корни 0 (кратности четыре) и 1 (кратности два). Поэтому общим решением исходного дифференциального уравнения является функция 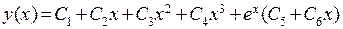 .
.
в) Простой комплексный корень. При решении алгебраического уравнения с вещественными коэффициентами наличие комплексного корня 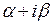 обеспечивает наличие комплексно сопряженного корня
обеспечивает наличие комплексно сопряженного корня 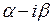 . Поэтому можно было бы в качестве частных решений, соответствующих этой паре корней, взять функции
. Поэтому можно было бы в качестве частных решений, соответствующих этой паре корней, взять функции 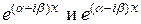 . Однако для того, чтобы не привлекать комплексные числа для решения дифференциальных уравнений с вещественными коэффициентами, используя формулу Эйлера
. Однако для того, чтобы не привлекать комплексные числа для решения дифференциальных уравнений с вещественными коэффициентами, используя формулу Эйлера 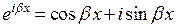 , в качестве частных решений берут функции
, в качестве частных решений берут функции 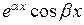 и
и 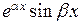 .
.
П р и м е р. Решить дифференциальное уравнение  . Характеристическим уравнением является уравнение
. Характеристическим уравнением является уравнение 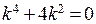 . Корнями этого уравнения являются
. Корнями этого уравнения являются 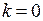 (кратности 2) и комплексные корни
(кратности 2) и комплексные корни 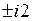 . Поэтому общее решение имеет вид
. Поэтому общее решение имеет вид 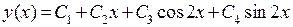 .
.
г) Комплексные корни кратности 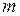 . В случае, когда характеристическое уравнение имеет два комплексно сопряженных корня
. В случае, когда характеристическое уравнение имеет два комплексно сопряженных корня 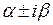 кратности
кратности 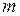 , соответствующие этим корням частные решения соответствующего однородного дифференциального уравнения имеют вид
, соответствующие этим корням частные решения соответствующего однородного дифференциального уравнения имеют вид 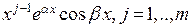 , и
, и 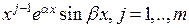 .
.
П р и м е р. Решить дифференциальное уравнение 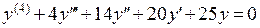 . Характеристическое уравнение можно представить в виде
. Характеристическое уравнение можно представить в виде 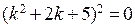 , следовательно, корнями характеристического уравнения являются
, следовательно, корнями характеристического уравнения являются 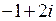 (кратности 2) и
(кратности 2) и 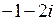 (кратности 2). Поэтому общим решение заданного однородного дифференциального уравнения будет функция
(кратности 2). Поэтому общим решение заданного однородного дифференциального уравнения будет функция 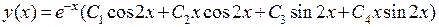 .
.
Решение неоднородного уравнения. Мы уже знаем, как найти общее решение однородного уравнения. Чтобы найти общее решение неоднородного уравнения, нужно найти частное решение неоднородного уравнения и прибавить к нему уже найденное общее решение соответствующего однородного уравнения. Действительно, пусть 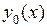 – общее решение однородного уравнения
– общее решение однородного уравнения 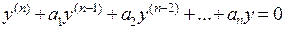 , содержащее
, содержащее  произвольных постоянных
произвольных постоянных 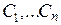 . Если
. Если 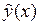 удовлетворяет неоднородному уравнению
удовлетворяет неоднородному уравнению 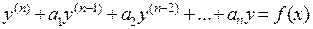 , то функция
, то функция 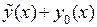 удовлетворяет тому же неоднородному уравнению и содержит произвольные постоянные
удовлетворяет тому же неоднородному уравнению и содержит произвольные постоянные 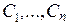 .
.
Таким образом, вопрос о нахождении общего решения неоднородного уравнения сводится к вопросу о нахождении частного решения неоднородного уравнения. Существуют разные методы построения такого решения. Рассмотрим метод вариации произвольной постоянной, который позволяет сразу получить общее решение неоднородного уравнения.
Суть этого метода в том, что, получив решение соответствующего однородного уравнения в виде 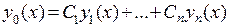 , мы ищем общее решение неоднородного уравнения в виде
, мы ищем общее решение неоднородного уравнения в виде 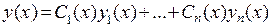 и подбираем такие неизвестные функции
и подбираем такие неизвестные функции 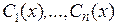 , чтобы функция
, чтобы функция 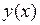 удовлетворяла неоднородному уравнению. Оказывается, что для этого достаточно, чтобы эти производные этих неизвестных функций удовлетворяли системе
удовлетворяла неоднородному уравнению. Оказывается, что для этого достаточно, чтобы эти производные этих неизвестных функций удовлетворяли системе
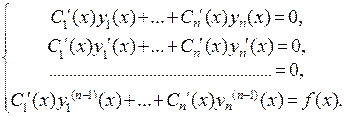
Докажем это для случая 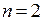 . Пусть необходимо решить уравнение
. Пусть необходимо решить уравнение 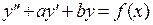 . Решение однородного уравнения имеет вид
. Решение однородного уравнения имеет вид 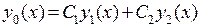 , причем
, причем 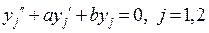 . Возьмем общее решение неоднородного уравнения в виде
. Возьмем общее решение неоднородного уравнения в виде 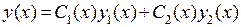 и подставим в неоднородное уравнение. Мы получим:
и подставим в неоднородное уравнение. Мы получим:
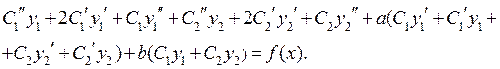
Выражения, имеющие сомножителями 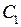 и
и 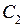 обращаются в ноль, поэтому имеем:
обращаются в ноль, поэтому имеем:
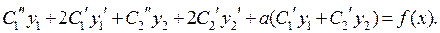
Пусть 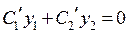 . Взяв производные от обеих частей этого равенства, получим
. Взяв производные от обеих частей этого равенства, получим 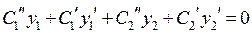 . Поэтому для того, чтобы функция
. Поэтому для того, чтобы функция 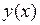 была решением неоднородного уравнения, остается положить
была решением неоднородного уравнения, остается положить 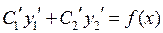 .
.
П р и м е р. Решить дифференциальное уравнение 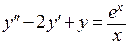 . Характеристическое уравнение для соответствующего однородного уравнения имеет вид
. Характеристическое уравнение для соответствующего однородного уравнения имеет вид 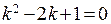 . Следовательно, общее решение однородного уравнения – функция
. Следовательно, общее решение однородного уравнения – функция 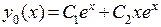 . Поэтому общее решение неоднородного уравнение ищем в виде
. Поэтому общее решение неоднородного уравнение ищем в виде 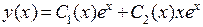 . Для определения неизвестных функций
. Для определения неизвестных функций 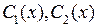 составим систему относительно их производных
составим систему относительно их производных
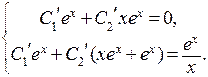
Сокращая уравнения на 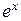 , мы получим систему с главным определителем, равным 1. Решая систему и интегрируя, получим
, мы получим систему с главным определителем, равным 1. Решая систему и интегрируя, получим 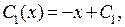
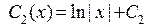 . Общее решение исходного уравнения запишется теперь в виде
. Общее решение исходного уравнения запишется теперь в виде 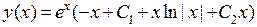 . Заметим, что в силу произвольности константы
. Заметим, что в силу произвольности константы 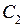 выражение
выражение 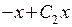 можно заменить выражением
можно заменить выражением 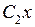 . Поэтому решение можно записать в виде
. Поэтому решение можно записать в виде 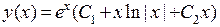 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Анализ бюджетов с использованием финансовых относительных показателей | | | ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ |
Дата добавления: 2014-11-24; просмотров: 327; Нарушение авторских прав

Мы поможем в написании ваших работ!